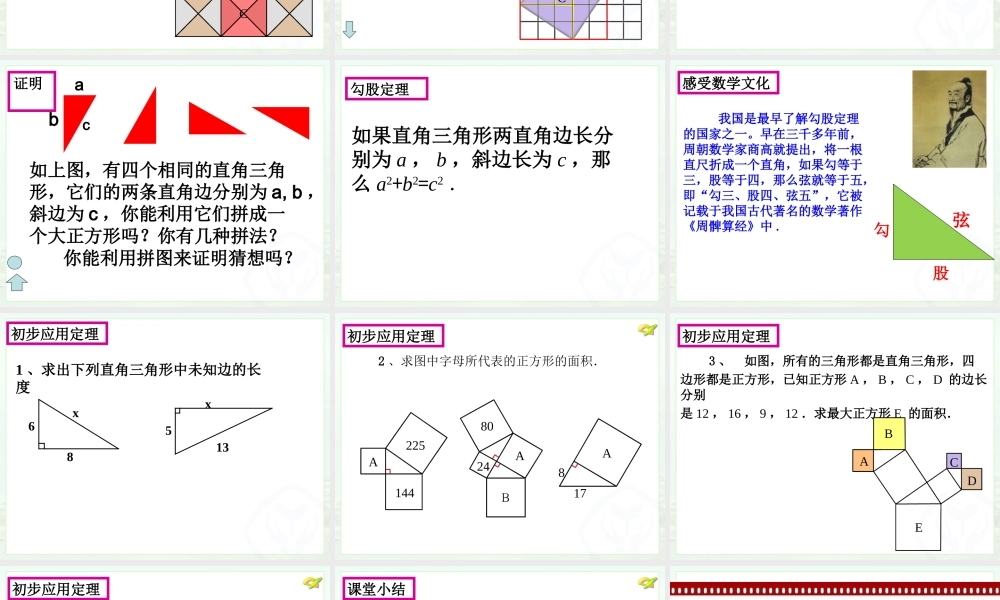
八年级 下册17.1 勾股定理( 1 ) 国际数学家大会是最高水平的全球性数学科学学术会议. 2002 年在北京召开了第 24 届国际数学家大会.如图就是大会的会徽的图案.创设情境 引入课题 相传 2500 年前,毕达哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.观察 (2) 由这三个正方形A , B , C 的边长构成的等腰直角三角形三条边长度之间有怎样的特殊关系?思考 问题 1(1) 三个正方形 A , B , C 的面积有什么关系? A B C (2) 正方形 A 、 B 、 C 所围成的直角三角形三条边之间有怎样的特殊关系?探究 问题 2 (1) 在网格中的一般的直角三角形,以它的三边为边长的三个正方形 A 、 B 、 C 是否也有类似的面积关系?为什么?A B C 猜想: 如果直角三角形两直角边长分别为 a ,b ,斜边长为 c ,那么 a2+b2=c2 .猜想 问题 3 通过前面的探究活动,猜一猜,直角三角 形三边之间应该有什么关系? 如上图,有四个相同的直角三角形,它们的两条直角边分别为 a, b ,斜边为 c ,你能利用它们拼成一个大正方形吗?你有几种拼法?abc证明 你能利用拼图来证明猜想吗?如果直角三角形两直角边长分别为 a , b ,斜边长为 c ,那么 a2+b2=c2 .勾股定理 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中 .感受数学文化勾弦股1 、求出下列直角三角形中未知边的长度68x5x13初步应用定理初步应用定理2 、求图中字母所代表的正方形的面积. A A A B 225 144 80 24 17 8 初步应用定理 3 、 如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形 A , B , C , D 的边长分别是 12 , 16 , 9 , 12 .求最大正方形 E 的面积. A B C D E 初步应用定理 通过这种方法,可以把一个正方形的面积分成若干 个小正方形的面积的和,不断地分下去,就可以得到一 棵美丽的勾股树.课堂小结 1 、在探究勾股定理的过程中,我们经历了怎样的探究过程?2 、在探究过程中,主要体现了哪些数学思想方法?3 、你还想了解哪些知识?勤奋 2+ 方法 2 = 成功 2课后作业 作业: 1 .整理课堂中所提到的勾股定理的证明方法;2 .通过上网等方法查找勾股定理的有关史料、趣事 及其他证明方法.