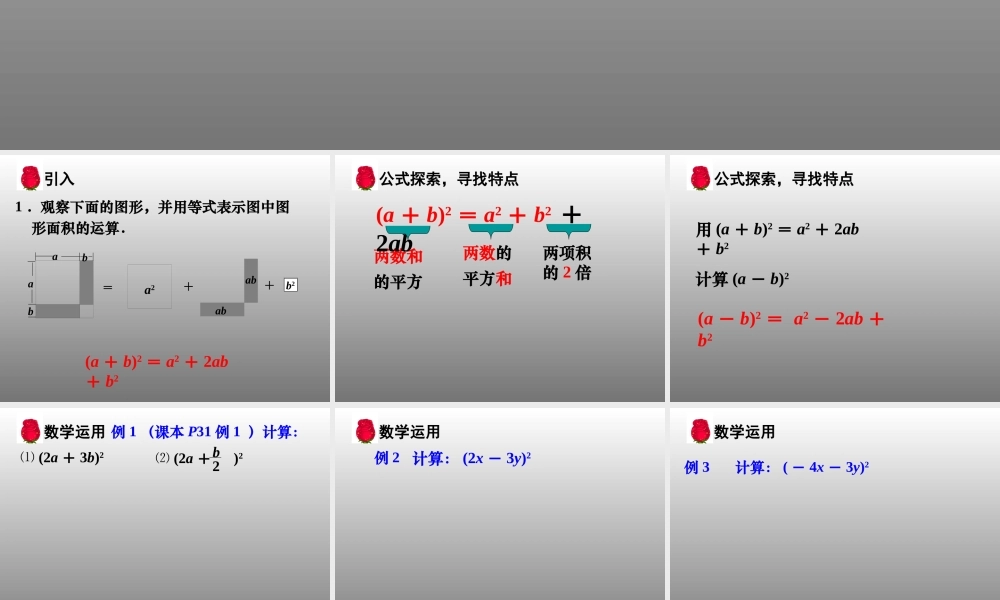
两数和的平方1 .观察下面的图形,并用等式表示图中图形面积的运算.=a2b2++ababababb2(a + b)2 = a2 + 2ab+ b2 引入两数和的平方公式探索,寻找特点(a + b)2 = a2 + b2 +2ab两数的平方和两项积的 2 倍 用 (a + b)2 = a2 + 2ab+ b2计算 (a - b)2(a - b)2 = a2 - 2ab +b2 公式探索,寻找特点例 1 (课本 P31 例 1 )计算: ⑴ (2a + 3b)2 ⑵ (2a + )2b2数学运用计算: (2x - 3y)2数学运用例 2 例 3 计算: ( - 4x - 3y)2数学运用计算:1 . (3x + 4)22 . (2x + y)2123 . ( - 2a + 3b)2124 . ( - x - 2y2)2 练习= (2000 - 1)2 例 4 计算: 19992= 20002 - 2×2000×1 + 12 解: 19992= 4000000 - 4000 + 1 = 3996001 数学运用例 5 计算: (a + b + c)2解: (a + b + c)2= (a + b)2 + 2(a + b)·c + c2 = a2 + 2ab + b2 + 2ac + 2bc + c2 = a2 + b2 + c2 + 2ab + 2ac +2bc 数学运用例 6 填空:1 . ( + )2 = a2 + +16b2 a4b8ab2 . (3x - )2 = 9x2 - 12xy+ 2y4y23 . (x + 4)2 = (x - 4)2 + 16x数学运用计算:1 . 30223 . (a + 2b - 3c)22 . ( - x + )2 + (x+ )21212 练习 已知 a2 + b2 = 1 , a - b = , 求 ab 与 a+b 的值12巩固提高1 .本节课在初步理解和掌握两数和的平方公式的基础上对两数和(差)的平方公式进行了强化和深化,使学生能灵活掌握两数和(差)的平方公式.2 .对于三个数或式子的平方可以先把一部份作为一个整体,经过两次平方来计算,或者直接应用三数的平方公式进行计算. 反思