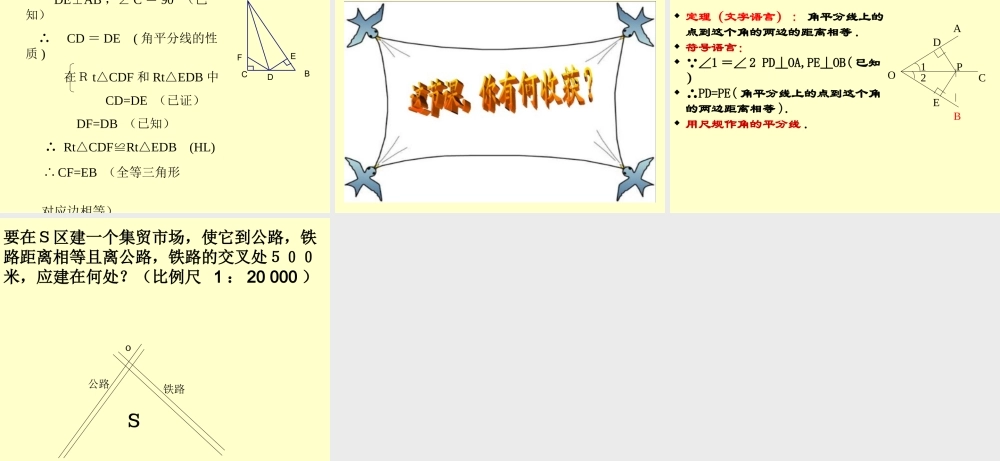
12.3.1 角平分线的性质1 学习目标:学习目标: 1. 通过操作、验证等方式, 掌握角平分线的性质定理 2. 能运用角的平分线性质定理 解决简单的几何问题 . 复习提问1 、角平分线的概念一条射线一条射线 把一个角把一个角 分成两个相等的角,分成两个相等的角,这条射线叫做这个角的平分线。这条射线叫做这个角的平分线。oBCA12 2. 下图中能表示点 P 到直线 l 的距离的是线段 PC 的长 如图 , 是一个平分角的仪器 , 其AB=AD,BC=DC. 将点 A 放在角的顶点 ,AB 和 AD沿着角的两边放下 , 沿 AC 画一条射线 AE,AE 就是角平分线 . 你能说明它的道理吗 ?经过上面的探索,你能得到作已知角的平分线的方法吗?小组内互相交流一下吧!探究 1--- 想一想 AABBMMNNCC 作法 :⑴ 以 O 为圆心 , 任意长为半径作弧 , 交 OA 于 M, 交 OB 于N.⑵ 分别以 M,N 为圆心 , 大于 的长为半径作弧 , 两弧在∠ AOB 的内部交于点 C.⑶ 作射线 OC,射线 OC 即为所求 .12 MN0温馨提示 : 作角平分线是最基本的尺规作图 , 大家一定要掌握噢 !试一试由上面的探究可以得出作已知角的平分线的方法已知 :AOB.∠求作 :AOB∠的平分线 . 1 〉平分平角∠ AOB2 〉通过上面的步骤,得到射线 OC 以后,把它反向延长得到直线 CD ,直线 CD 与直线 AB 是什么关系? 3 〉结论:作平角的平分线即可平分平角,由此也得到过直线上一点作这条直线的垂线的方法。ABOCD 已知: OC 是∠ AOB 的平分线,点 P 在 OC 上, PD OA ⊥, PE OB⊥,垂足分别是 D 、E. 求证: PD=PE.AOBPEDC 角平分线上的点到角的两边的距离相等你能用文字语言叙述一下发现的结论吗?说一说AOBPEDPD OA ⊥, PE OB⊥ OP 平分∠ AOB∴PD=PE.用符号表示为: 角平分线的性质角的平分线上的点到角的两边的距离相等。角的平分线上的点到角的两边的距离相等。BADOPEC定理应用所具备的条件: ( 1 )角的平分线;( 2 )点在该平分线上; ( 3 )垂直距离。定理的作用: 证明线段相等。 1 、如图 , △ABC 的角平分线 BM,CN 相交于点 P,求证:点 P 到三边 AB 、 BC 、 CA 的距离相等ABCPMNDEF证明:过点 P 作 PDAB⊥于 D , PE⊥BC 于 E , PFAC⊥于 F BM 为△ ABC 的角平分线∴PD=PE同理 ,PE=PF. ∴PD = PE=PF即点 P 到三边 AB 、 BC 、 CA...