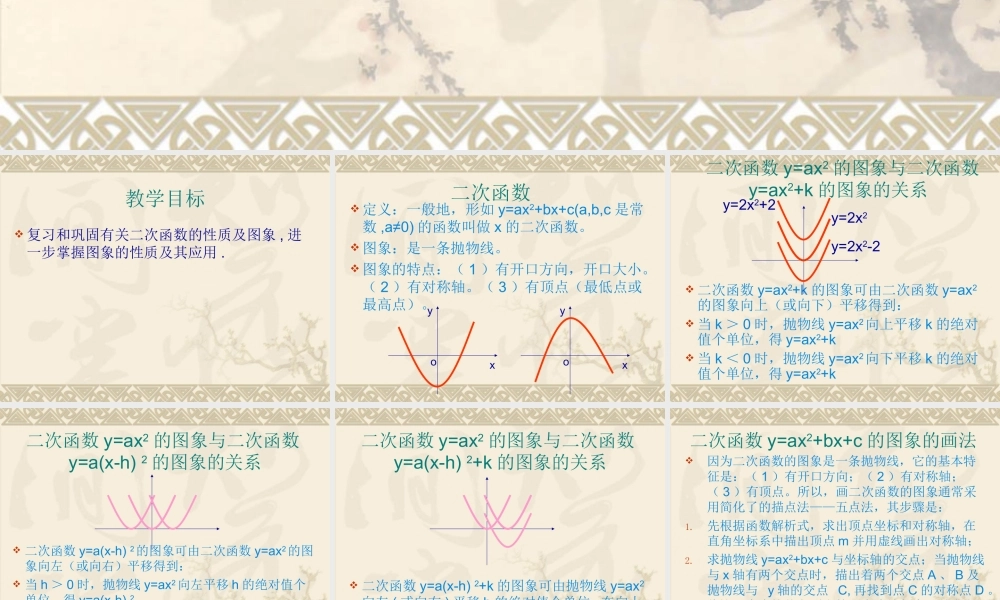
九年级数学下册二次函数回顾与思考白银市二中 张艳梅 教学目标 复习和巩固有关二次函数的性质及图象 , 进一步掌握图象的性质及其应用 . 二次函数 定义:一般地,形如 y=ax2+bx+c(a,b,c 是常数 ,a≠0) 的函数叫做 x 的二次函数。 图象:是一条抛物线。 图象的特点:( 1 )有开口方向,开口大小。( 2 )有对称轴。( 3 )有顶点(最低点或最高点)。oxyoxy 二次函数 y=ax2 的图象与二次函数y=ax2+k 的图象的关系 二次函数 y=ax2+k 的图象可由二次函数 y=ax2的图象向上(或向下)平移得到: 当 k > 0 时,抛物线 y=ax2向上平移 k 的绝对值个单位,得 y=ax2+k 当 k < 0 时,抛物线 y=ax2向下平移 k 的绝对值个单位,得 y=ax2+ky=2x2y=2x2-2y=2x2+2 二次函数 y=ax2 的图象与二次函数y=a(x-h) 2 的图象的关系 二次函数 y=a(x-h) 2的图象可由二次函数 y=ax2的图象向左(或向右)平移得到: 当 h > 0 时,抛物线 y=ax2向左平移 h 的绝对值个单位,得 y=a(x-h) 2 当 h < 0 时,抛物线 y=ax2向右平移 h 的绝对值个单位,得 y=a(x-h) 2 二次函数 y=ax2 的图象与二次函数y=a(x-h) 2+k 的图象的关系 二次函数 y=a(x-h) 2+k 的图象可由抛物线 y=ax2向左 ( 或向右 ) 平移 h 的绝对值个单位 , 在向上( 或向下 ) 平移 k 的绝对值个单位而得到 . 二次函数 y=ax2+bx+c 的图象的画法因为二次函数的图象是一条抛物线,它的基本特征是:( 1 )有开口方向;( 2 )有对称轴;( 3 )有顶点。所以,画二次函数的图象通常采用简化了的描点法——五点法,其步骤是:1.先根据函数解析式,求出顶点坐标和对称轴,在直角坐标系中描出顶点 m 并用虚线画出对称轴;2.求抛物线 y=ax2+bx+c 与坐标轴的交点;当抛物线与 x 轴有两个交点时,描出着两个交点 A 、 B 及抛物线与 y 轴的交点 C, 再找到点 C 的对称点 D 。将这五个点按从左到右的顺序连结起来,并向上或向下延伸,就得到二次函数的图象。 二次函数 y=ax2+bx+c 的性质 当 a0﹥ 时:抛物线开口向上。 对称轴是 x=- , 顶点坐标是 ( - , ) 当 a0﹥ 时 , 在对称轴的左侧,即当 x < - 时, y 随 x 的增大而减小; 在对称轴的右侧,即当 x - ﹥时, y 随x 的增大而增大。简记左减右增。抛物线有最低点,当 x=- ...