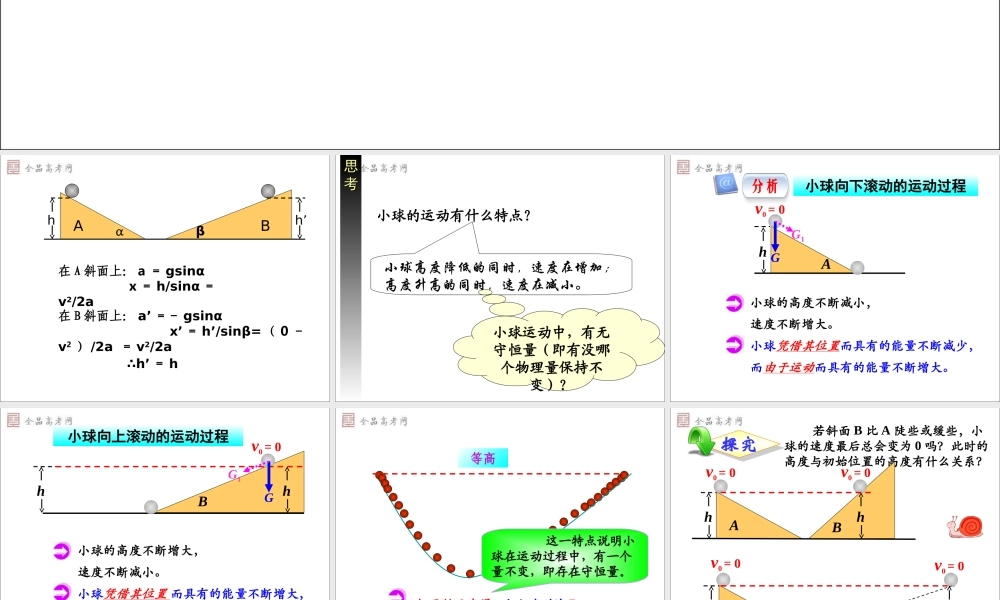
7.1 7.1 追寻守恒量追寻守恒量第七章 机械能守恒定律在 A 斜面上: a = gsinα x = h/sinα =v2/2a ABhh’αβ在 B 斜面上: a’ =- gsinα x’ = h’/sinβ= ( 0 -v2 ) /2a = v2/2a∴h’ = h小球的运动有什么特点?小球高度降低的同时,速度在增加;高度升高的同时,速度在减小。思思考考小球运动中,有无守恒量(即有没哪个物理量保持不变)?小球的高度不断减小,速度不断增大。小球凭借其位置而具有的能量不断减少,而由于运动而具有的能量不断增大。分析Ahv0 = 0小球向下滚动的运动过程GG1小球的高度不断增大,速度不断减小。小球凭借其位置 而具有的能量不断增大,而由于运动 而具有的能量不断减小,Bhv0 = 0小球向上滚动的运动过程hGG1等高如果斜面光滑,当小球到达 B斜面的 h 高度时,速度为 0 。 这一特点说明小球在运动过程中,有一个量不变,即存在守恒量。 若斜面 B 比 A 陡些或缓些,小球的速度最后总会变为 0 吗?此时的高度与初始位置的高度有什么关系?探究ABhv0 = 0ABhv0 = 0v0 = 0v0 = 0hh 通过以上实验我们可以观察到斜面上的小球、单摆中的小球、滚摆中的轮子好像“记得 ”自己起始的高度(或与高度相关的某个量)。 后来的物理学家把这一事实说成是“某个量是守恒的” ,并且把这个量叫做能量或能。 在伽利略斜面实验中,将小球提高到起始点的高度时,小球被赋予一种形式的能量——势能。 相互作用的物体凭借其位置而具有的能量叫做势能( potential energy )。名词解释ABhv0 = 0参考面它们具有势能球杠铃被弹高的人 物体由于运动而具有的能量叫做动能( kinetic energy )。名词解释探究ABhv0 = 0小球在全部运动过程中,能量是怎样转化的?用“能量”描述伽利略斜面实验 当小球由最高点沿斜面 A 运动到达最低点时,能量怎样变化?想一想ABhv0 = 0势能消失动能全部参考面速度最大高度为 0小球到达最低点(参考面)势能去了哪里?用“能量”描述伽利略斜面实验 当小球由最低点继续沿斜面B升高时,能量有何变化?想一想ABhv0 = 0动能减小势能增大高度变大速度变小不断失去动能势能不断被“回收”用“能量”描述伽利略斜面实验ABhv0 = 0h 当小球沿斜面 B 上升,速度变为0时,能量有何变化?想一想v0 = 0动能消失势能全部高度最大速度为 0起始高度 h =动能去了哪里?用“能量”描述伽利略斜面实验回顾用“力”描述伽...