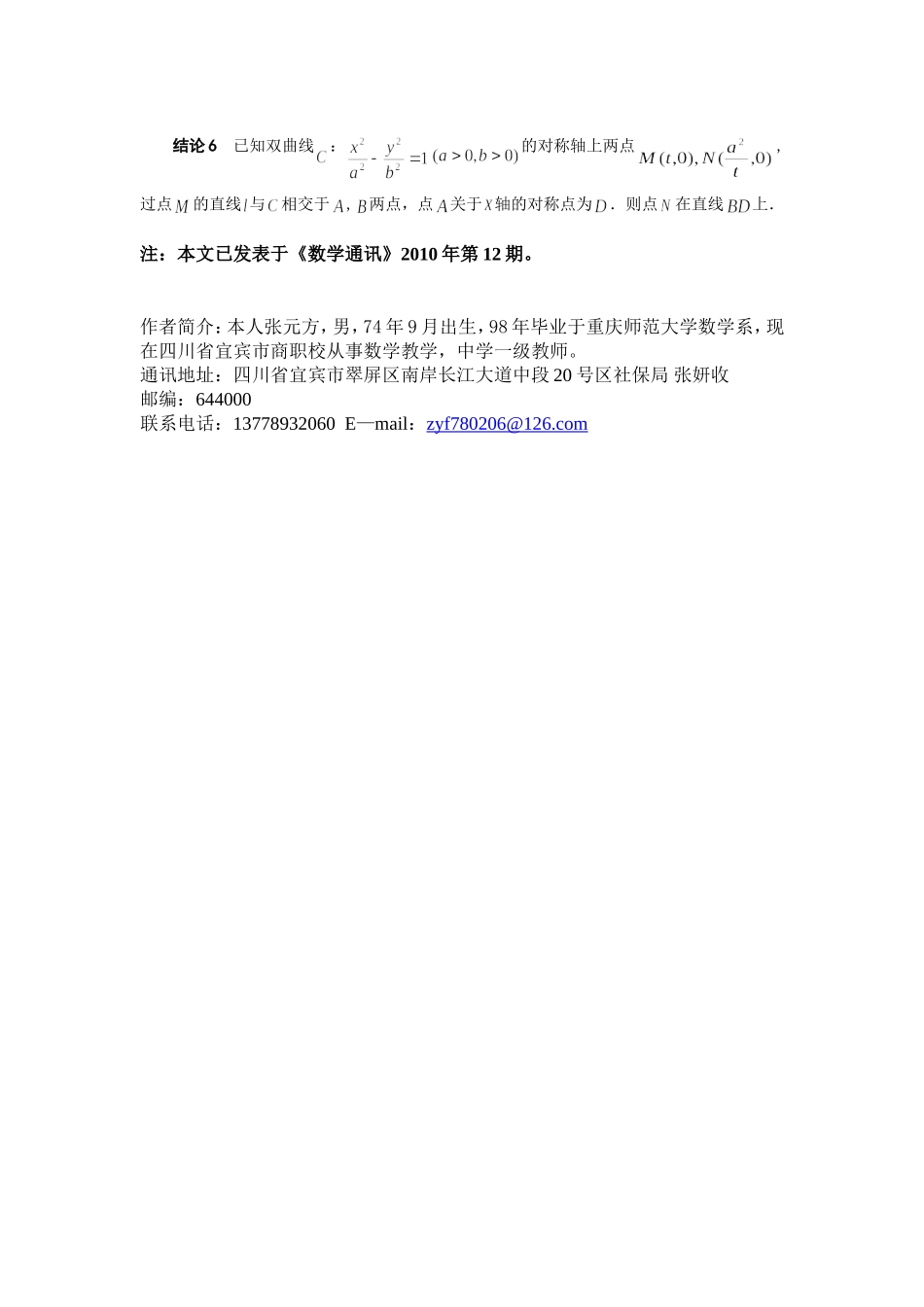
一道高考题的探究性学习张元方(四川省宜宾市商职校 644000)一道好的高考题总会留下很大的拓展空间,让你产生无尽的遐想,细细品来,令人回味无穷.2010 年高考全国卷(Ⅰ)理科第 21 题第(1)问就是这样的好题:已知抛物线:的焦点为,过点的直线 与相交于,两点,点关于 轴的对称点为.(1)证明:点在直线上;(2)略.笔者就此问题展开探讨,得到如下一些优美的结论.结论 1 已知抛物线:的焦点为,过点的直线 与相交于,两点,点关于 轴的对称点为.则点在直线上.证明 设, 的方程为,则直线的方程为,即.令,得.将代入并整理得,从而.又,,将两式代入得.所以点在直线上.结论 2 已知椭圆:的一个焦点为,相应的一条准线与 轴的交点为,过点的直线 与相交于,两点,点关于 轴的对称点为.则点在直线上.证明 (我们以右焦点和右准线为例)设, 的方程为,则直线的方程为,即.令,得.将代入并整理得,从而,.又,,将以上四式 代 入得.所以点在直线上.结论 3 已知双曲线:的一个焦点为,相应的一条准线与轴的交点为,过点的直线 与相交于,两点,点关于 轴的对称点为.则点在直线上.证明 (我们以右焦点和右准线为例)设, 的方程为,则直线的方程为,即.令,得.将代入并整理得,从而,.又,,将以上四式先后代入得.所以点在直线上.同样的方法,还可以得到如下更一般性结论(以下 皆为常数):结论 4 已知抛物线:的对称轴 轴上两点,过点的直线 与相交于,两点,点关于 轴的对称点为.则点在直线上.结论 5 已知椭圆:的对称轴上两点,过点的直线 与相交于,两点,点关于 轴的对称点为.则点在直线上.结论 6 已知双曲线:的对称轴上两点,过点的直线 与相交于,两点,点关于 轴的对称点为.则点在直线上.注:本文已发表于《数学通讯》2010 年第 12 期。作者简介:本人张元方,男,74 年 9 月出生,98 年毕业于重庆师范大学数学系,现在四川省宜宾市商职校从事数学教学,中学一级教师。通讯地址:四川省宜宾市翠屏区南岸长江大道中段 20 号区社保局 张妍收 邮编:644000联系电话:13778932060 E—mail:zyf780206@126.com