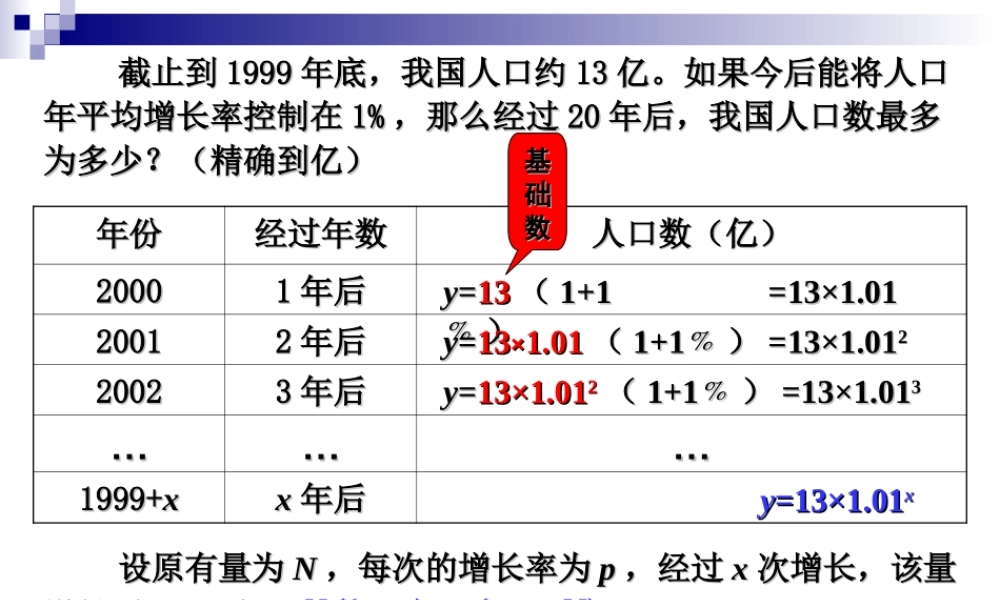
截止到截止到 19991999 年底,我国人口约年底,我国人口约 1313 亿。如果今后能将人口亿。如果今后能将人口年平均增长率控制在年平均增长率控制在 1%1% ,那么经过,那么经过 2020 年后,我国人口数最多年后,我国人口数最多为多少?(精确到亿) 为多少?(精确到亿) 年份年份经过年数经过年数人口数(亿)人口数(亿)2000200011 年后年后2001200122 年后年后2002200233 年后年后………………1999+1999+xxxx 年后年后yy==1313 (( 1+11+1﹪﹪ ))=13×1.01=13×1.01yy==1313××1.011.01 (( 1+1﹪1+1﹪ )) =13×1.01=13×1.0122yy==13×1.0113×1.0122 (( 1+1﹪1+1﹪ )) =13×1.01=13×1.0133yy=13×1.01=13×1.01xx基基础础数数 设原有量为设原有量为 NN ,每次的增长率为,每次的增长率为 pp ,经过,经过 xx 次增长,该量次增长,该量增长到增长到 y y ,则 ,则 .. y y = = NN (1 + (1 + pp) ) xx ( ( xx ∈ ∈ N)N) yy = = kakaxx ( (kk R∈ R∈且且 kk ≠ 0 ≠ 0 ;; aa > 0 > 0 且且 aa ≠ ≠ 1)1) 指数型函数:指数型函数: ★★ 求函数的解析式的方法:求函数的解析式的方法: 11 、待定系数法、待定系数法一次函数:一次函数: yy==kxkx++b b ((kk≠0)≠0)二次函数:一般式 二次函数:一般式 yy==axax22++bxbx++c c ((aa≠0)≠0) 顶点式 顶点式 yy==aa((xx -- kk))22++h h ((aa≠0)≠0) 双根式 双根式 yy==aa((xx--xx11)()(xx--xx22) ) ((aa≠0)≠0)反比例函数:反比例函数:指数函数:指数函数: yy==aaxx ((aa>0>0 且且 aa≠1)≠1)指数型函数:指数型函数: yy==kakax x ((kk ≠ 0 ≠ 0 ;; aa>0>0 且且 aa≠1)≠1)0kxky 人口问题是全球性问题,由于全球人口人口问题是全球性问题,由于全球人口迅猛增加,已引起全世界关注.世界人口迅猛增加,已引起全世界关注.世界人口 20020000 年大约是年大约是 6060 亿,而且以每年亿,而且以每年 1.3%1.3% 的增长率的增长率增长,按照这种增长速度,到增长,按照这种增长速度,到 20502050 年世界人年世界人口将达到口将达到 100100 多亿,大有“人口爆炸”的趋多亿,大有“人口爆炸”的趋势.为此,全球范围内敲起了人口警钟,并势.为此,全球范围内敲起了人口警钟,并把每年的把每年的 77 月月 1111 日定为“世界人口日”...