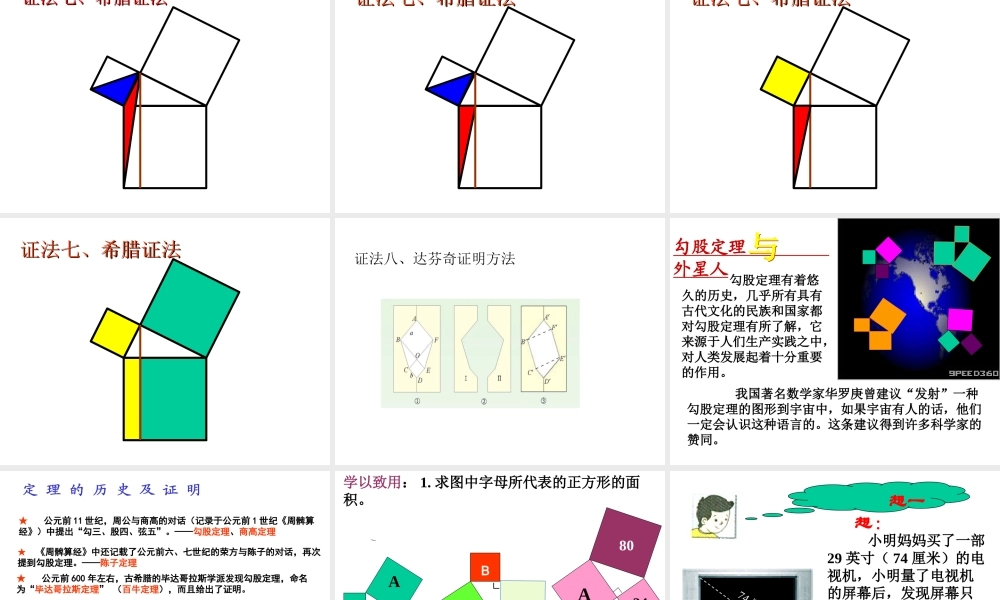
18.1 勾股定理( 1 )地砖铺成的地面BCA acb相传 2500 年前 , 古希腊有一位非常著名的数学家毕达哥拉斯 ,他善于观察和思考问题 , 经常从生活中寻找一些数学问题 ,有一次 , 他到朋友家做客 , 发现朋友家的用砖铺成的地面中反映了直角三角形三边的某种数量关系 . AB网格中的直角三角形是否也有这样的性质呢 ? ( 每个小方格的边长都是 1 个单位长度 ) CA 的面积( 单位面积 )B 的面积( 单位面积 )C 的面积( 单位面积 )91625abc 图 2abc猜想:直角三角形的两直角边长 分别为 a 、 b ,斜边长为 c , 那么baca2+b2=c2 。acb┐图 1baabc剪一剪 拼一拼剪一剪 拼一拼 你能把图你能把图 11 拼成图拼成图 22的样子吗的样子吗 ?? 如果直角三角形的两直角边长分别为a、b,斜边为c,那么 a2+b2=c2 。 勾股定理: 勾股弦abc赵爽弦图证法 证法一、 赵爽弦图验证勾股定理 s 大正方形 =222214)(baabababc而 s 大正方形 =c2 ∴a2+b2=c2 abc①②③④⑤证法二 无字证明无字证明 青出朱入朱出朱方青方青入青入青出青出证法三、青朱出入图朱入朱出 bababa bacccc(a+b)2 =a2 + b2 + 2ab = c2+2ab可得 : a2 + b2 = c2ab2142c证法四 aabbcc证法五、美国第 20 任总统伽菲尔德证法: s 梯形 = (a+b)(a+b)= (a2+2ab+b2) 2121212121s 梯形 =2× ab+ c2=ab+ c2212121 ∴ a2+ab+ b2=ab+ c2 ∴a2+b2=c22121= a2+ab+ b2 证法六、拼图游戏证法六、拼图游戏 证证法七、希腊证法法七、希腊证法 证证法七、希腊证法法七、希腊证法 证法七、希腊证法证法七、希腊证法 证法七、希腊证法证法七、希腊证法 证法七、希腊证法证法七、希腊证法 证法八、达芬奇证明方法 勾股定理有着悠久的历史,几乎所有具有古代文化的民族和国家都对勾股定理有所了解,它来源于人们生产实践之中,对人类发展起着十分重要的作用。 我国著名数学家华罗庚曾建议“发射”一种勾股定理的图形到宇宙中,如果宇宙有人的话,他们一定会认识这种语言的。这条建议得到许多科学家的赞同。 勾股定理 外星人 ★ 公元前 600 年左右,古希腊的毕达哥拉斯学派发现勾股定理,命名为“毕达哥拉斯定理” (百牛定理),而且给出了证明。★ 古巴比仑人在公元前 19 世纪也发现此定理。★ 定理从提出到现在的两千多年中,已经找到证明 400 多种,由鲁密斯搜集整理的《毕达哥...