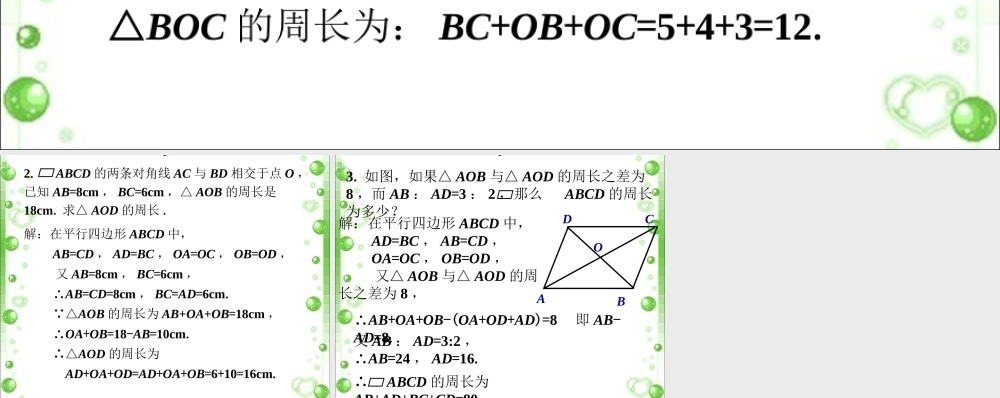
1. 在 ABCD 中,两条对角线 AC 与 BD 相交于点 O ,AB=4 , BC=5 , AC=6 , BD=8.△AOB 的周长和△ BOC 的周长 .解:在平行四边形 ABCD 中, AB=CD , AD=BC , OA=OC , OB=OD , 又 AB=4 , BC=5 , AC=6 , BD=8 , AB=CD=4 , AD=BC=5 , OA=OC=3 , OB=OD=4. ∴△AOB 的周长为: AB+OA+OB=4+3+4=11. △BOC 的周长为: BC+OB+OC=5+4+3=12.2. ABCD 的两条对角线 AC 与 BD 相交于点 O ,已知 AB=8cm , BC=6cm ,△ AOB 的周长是18cm. 求△ AOD 的周长 .解:在平行四边形 ABCD 中, AB=CD , AD=BC , OA=OC , OB=OD , 又 AB=8cm , BC=6cm , ∴AB=CD=8cm , BC=AD=6cm. ∵△AOB 的周长为 AB+OA+OB=18cm , ∴OA+OB=18-AB=10cm. ∴△AOD 的周长为 AD+OA+OD=AD+OA+OB=6+10=16cm.3. 如图,如果△ AOB 与△ AOD 的周长之差为8 ,而 AB : AD=3 : 2 ,那么ABCD 的周长为多少?ABDCO解:在平行四边形 ABCD 中, AD=BC , AB=CD , OA=OC , OB=OD , 又△ AOB 与△ AOD 的周长之差为 8 ,∴AB+OA+OB-(OA+OD+AD)=8 即 AB-AD=8.又 AB : AD=3:2 ,∴AB=24 , AD=16. ∴ABCD 的周长为AB+AD+BC+CD=80.