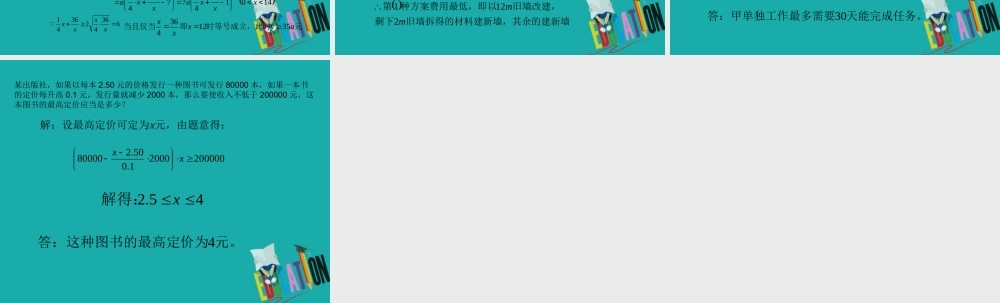
不等式的实际应用例 1 根据某乡镇家庭抽样调查的统计, 2003 年每户家庭年平均消费支出总额为 1万元,其中食品消费额为 0.6 万元。预测 2003 年后,每户家庭年平均消费支出总额每年增加 3000 元,如果 2005 年该乡镇居民生活状况能达到小康水平(即恩格尔系数 n 满足条件 40%0) ,则到 2005 年,食品消费额为 0.6(1+x)2 万元 ,消费支出总额为 1+2×0.3=1.6 万元。依题意得20.6(1)40%50%1.6x≤221530103610xxxx≤由 x>0 ,解得 4 151152 3013xx ≤因此 4 152 311153x≤练习 1 、 国家为了加强对烟酒生产的宏观管理,实行征收附加税政策.已知某种酒每瓶 70 元,不加收附加税时,每年大约销售 100 万瓶;若政府征收附加税,每销售 100 元要征税 R 元(叫做税率 R %),则每年的销售量将减少 10R 万瓶.要使每年在此项经营中所收取的附加税不少于 112 万元, R 应怎样确定?解:由题意得生产销售的酒为 (100 - 10R) 万瓶,可以卖得 70×(100 - 10R)万 元, 附加税为 70×(100 - 10R)×R% 万元,所以70×(100 - 10R)×R%≥112 ,即 R2 - 10R+16≤0 , 解得 2≤R≤8.答: R 的取值范围为 2≤R≤8 。例 2 :设计一幅宣传画,要求画面面积 4 840 cm2 ,画面的上、下各留 8 cm 的空白,左右各留 5 cm 的空白.怎样确定画面的高与宽的尺寸,能使宣传画所用纸张最小?解:设高为 x cm, 则宽 为宣传画所用纸张的总面积为:,x4840)104840()16(xxy160)48401610(4840xx67601016484025000xxcm558810x164840为时,等号成立,此时宽即当且仅当cmxx练习 2 :某工厂有旧墙 14 m ,现准备利用这面旧墙建造平面,图形为矩形,面积为 126 平方米的厂房,工程条件是: (1) 建 1 m 新墙的费用为 a 元; (2) 修 1m旧墙的费用是 a/4 元; (3) 拆去 1m 旧墙,用所得的材料建 1m 新墙的费用为 a/2 元。 经讨论有两种方案: (1) 利用旧墙的一段 x 米 (x<14) 为矩形厂房的一面的边长; (2) 矩形一面的边长 x≥14 米.问如何利用旧墙,即 x 为多少时建墙费用最省? mxxm126,则矩形的另一面边长为厂房的一...