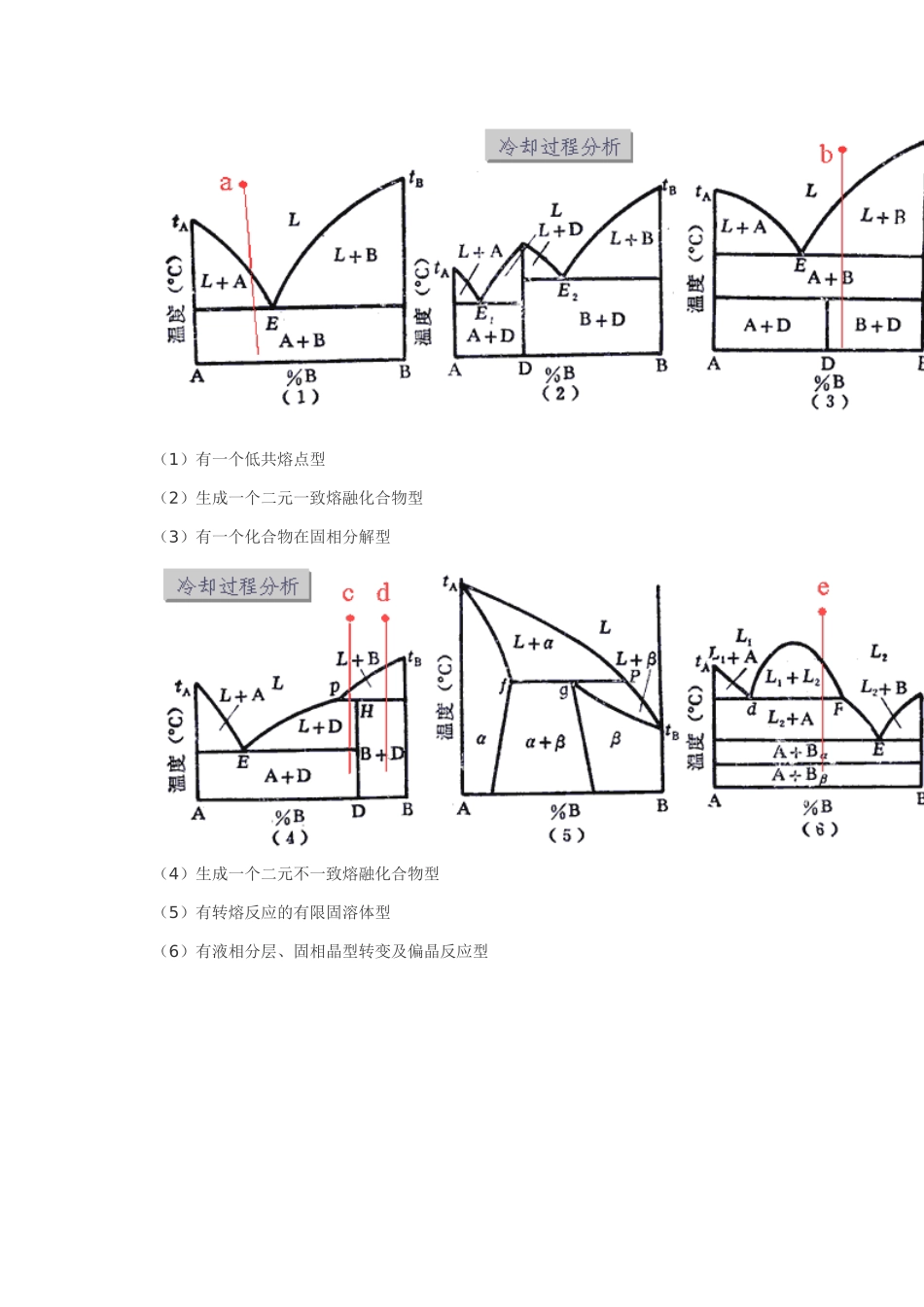
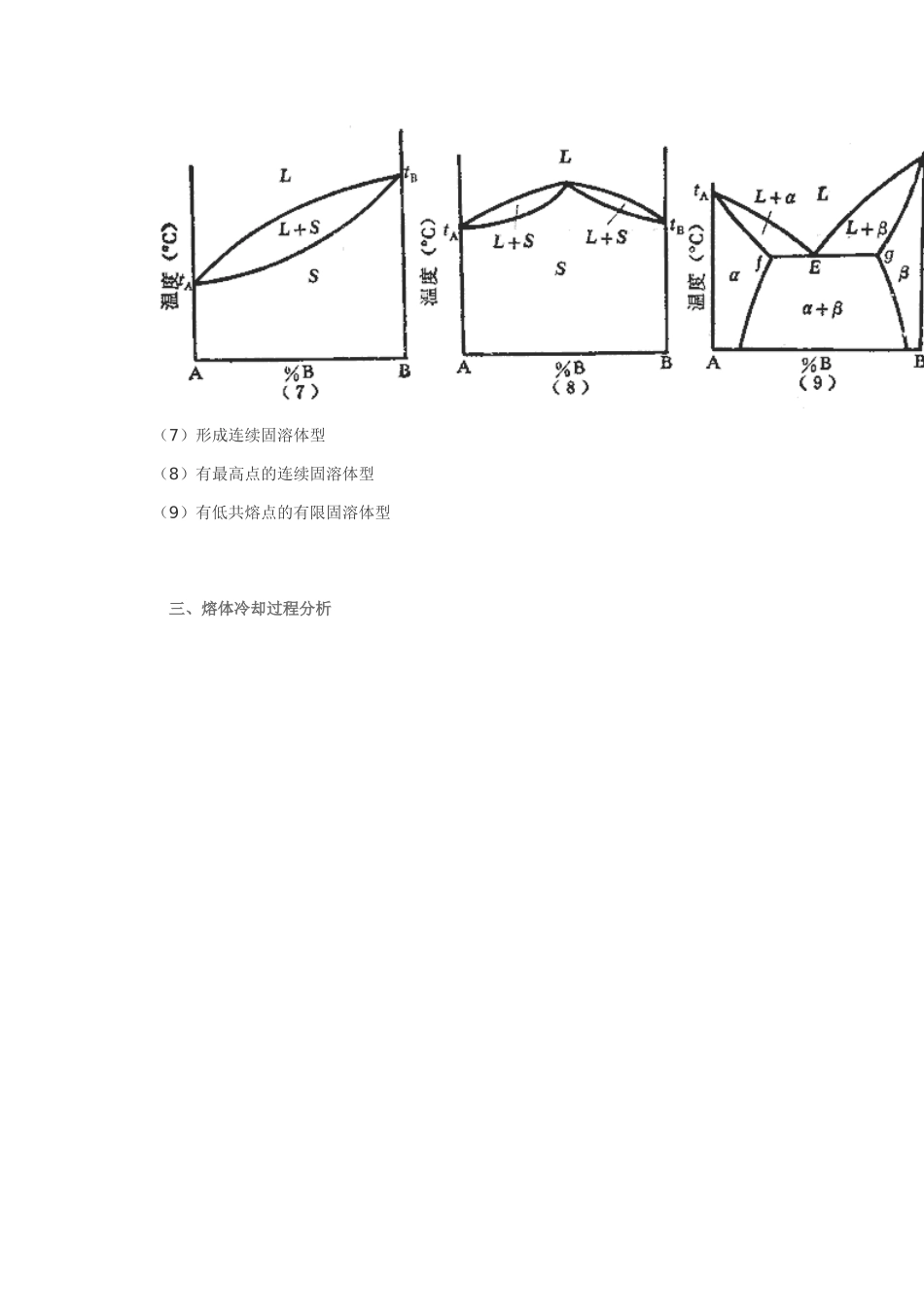
第二章 冶金熔体的相平衡图2.1 三元系相图基础知识 2.1.1 相律及二元系相图回顾 一、相律 描述平衡体系中独立组元数、相数和自由度数之间的关系f = c – Φ + 2 对于常压下的冶金熔体体系,可以忽略气相的影响f = c – Φ + 1 独立组元数 c与体系中物质种类数 N、独立化学反应数 R 和限制条件数 S 的关系:c = N – R – S 二、 二元系相图的基本类型 (1/3) (1)有一个低共熔点型(2)生成一个二元一致熔融化合物型(3)有一个化合物在固相分解型 (4)生成一个二元不一致熔融化合物型(5)有转熔反应的有限固溶体型(6)有液相分层、固相晶型转变及偏晶反应型 (7)形成连续固溶体型(8)有最高点的连续固溶体型(9)有低共熔点的有限固溶体型 三、熔体冷却过程分析 2.1.2 三元系的组成表示法 对于三元熔体体系:f = c – Φ + 1 = 4 – Φ 三元凝聚体系的自由度数最多为 3,即体系的平衡状态决定于温度和两个组元的浓度。 要完整地表示三元系的状态,必须采用三维空间图形。 在这种立体图中,底面上的两个坐标表示体系的组成,垂直于底面的坐标表示温度。 一、浓度三角形 → 等腰直角三角形表示法→ 等边三角形表示法 1、等腰直角三角形表示法 用纵轴表示组元 A 的浓度,横轴表示组元 B 的浓度,两轴均分为 100 等分。 组元 C 的含量 → 计算法:C% = 100 – A% – B% → 图解法: 过 M 点作斜边的平行线交 AC、BC 边 于 m2、m1; 线段 Am2 或 Bm1 的长度表示组元 C 的 含量。 → 优点:可以用普通直角坐标纸作图→ 缺点:坐标原点所表示组元的含量的读取欠方便 2、等边三角形表示法 性质:→ 吉布斯浓度三角形 → 罗策布浓度三角形 → 优点:可以直接从图上读出三个组元的百分含量→ 缺点:必须用等边三角形坐标纸 3、双线法确定体系的组成 二、浓度三角形的性质 1、等含量规则→ 在浓度三角形△ABC 中平行于三角形某一边的任一直线上,其所有体系点中对应顶点组元的浓度相等。如图:→ KK'线上诸物系点中组元 C 的含量均为 c%2、等比例规则 → 由浓度三角形中任一顶点向对边引一射线,则射线上所有各点含三角形其余二顶点所表示的组元的数量比例均相等。如图:→ b1/c1 = b2/c2 = b3/c3 = … = 常数3、背向规则→ 在浓度三角形△ABC 中,假定当物系点 P...