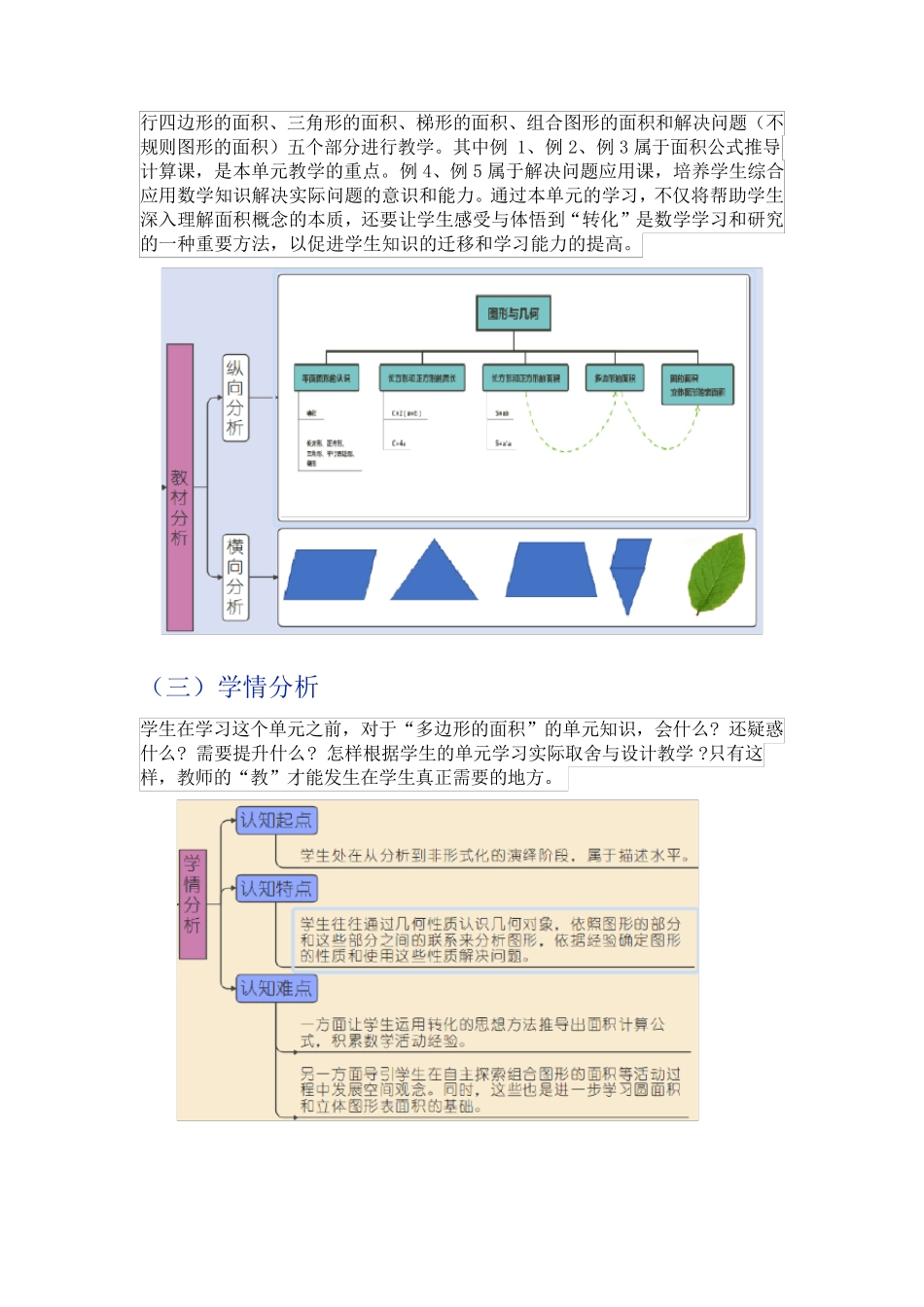
《多 边 形 的 面 积 》 大 单 元 教 学 设 计 ——基于教 学 评一体化的单 元 教 学 本 案 例 是 人 教 版 五 年 级 上 册 第 6 单 元 《 多 边 形 的 面 积 》 。 本 单 元 内 容 的 学 习 , 一 方面 让 学 生 学 会 转 化 的 思 想 方 法 , 推 导 出 面 积 计 算 公 式 , 积 累 数 学 活 动 经 验 。 另 一 方面 在 自 主 探 索 组 合 图 形 的 面 积 等 活 动 过 程 中 发 展 空 间 观 念 。 平 面 图 形 的 面 积 在 小 学几 何 模 块 内 容 中 占 据 了 很 大 的 比 重 , 在 教 科 书 中 主 要 运 用 了 拼 接 的 方 法 , 指 导 学 生探 究 面 积 公 式 的 形 成 过 程 。 对 学 生 来 说 利 用 公 式 求 平 面 图 形 的 面 积 不 是 难 事 , 在 一定 的 变 式 训 练 量 下 , 学 生 解 题 能 力 普 遍 得 以 提 高 , 但 是 对 于 学 生 来 说 , 仅 仅 会 用 公式 解 题 , 就 达 到 教 学 目 的 了 吗 ? 为 什么要 学 习 面 积 计 算 呀? 各种平 面 图 形 的 面 积 之间 的 内 在 联系等 更加有价值的 问题 在 课堂上 的 呈现, 将在 本 次课例 研究 中 进行重 点研究 。 单 元 整体教 学 设计 将从单 元 分析, 单 元 规划, 课时规划三个方 面 设计 。 一 、单 元 分析 (一 )课标分析: 课程 标准(2022)关于 本 单 元 的 要 求 , 从“内 容 要 求 ”“学 业要 求 ”“教 学 提 示”三个方 面 进行课标摘抄。 (二)教 材分析 纵向分析:“多 边 形 的 面 积 ”是 人 教 版 教 材五 年 级 上 册 第 六单 元 的 教 学 内 容 , 根据 教 材的 编排, 从一 年 级 下 册 开始依次编排了 以 下 内 容 。 可以 看出 , 本 单 元 “多边 形 的 面 积 ”起到 一 个承上 启下 的 作用 , 为 进一 步学 习 圆的 面 积 和立体图 形 的 表面 积 打下 基础。 横向分析:从单 元 内 容 分析, 本 单 元 将“多 边 形 的 面 积 ”分为 平行四边形的面积、三角形的面积、梯形的面积、组合图形的面积...