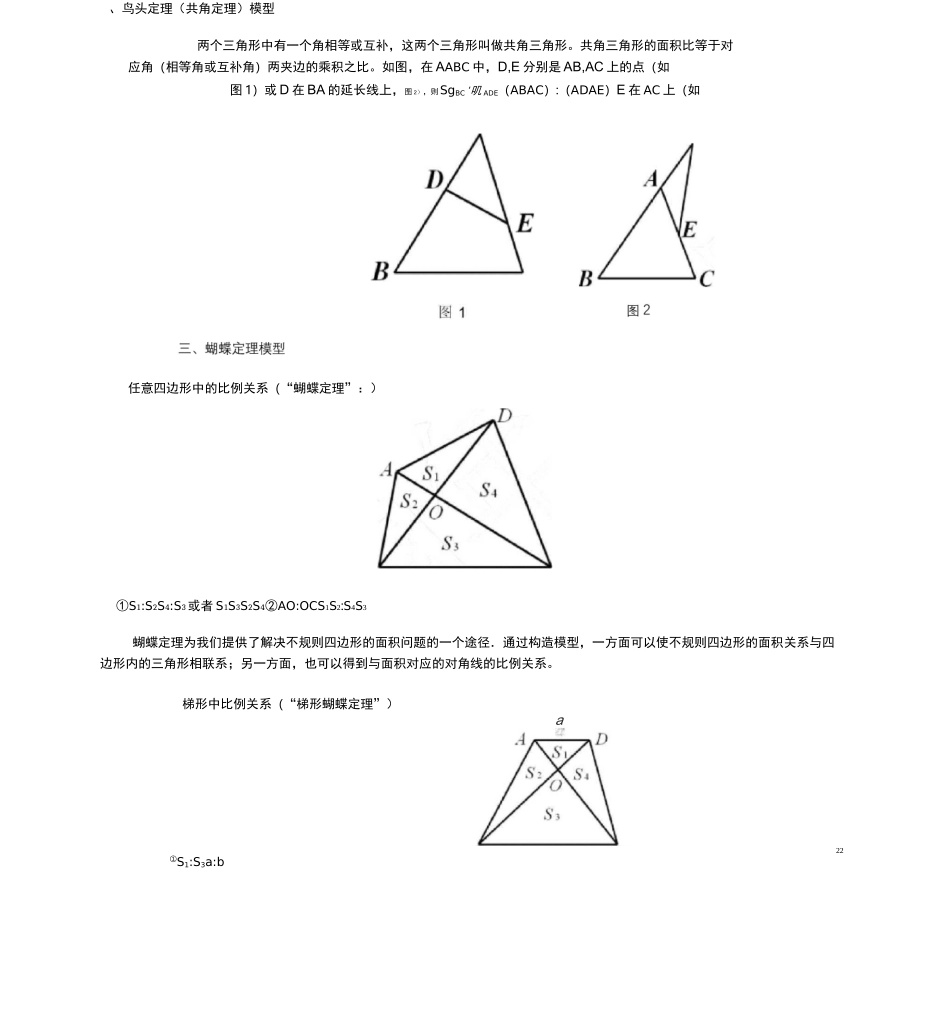
五大模、等积变换模型⑴ 等底等高的两个三角形面积相等;两个三角形底相等,面积比等于它们的高之比。如上图 S1:S2a:b⑶ 夹在一组平行线之间的等积变形,如下图 S^CD=S^CD;反之,如果 S ACD BCD△△(4)正方形的面积等于对角线长度平方的一半;22⑸ 三角形面积等于与它等底等高的平行四边形面积的一半;、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。如图,在 AABC 中,D,E 分别是 AB,AC 上的点(如图 1)或 D 在 BA 的延长线上,图 2),则SgBC'叽 ADE(ABAC):(ADAE)E 在 AC 上(如任意四边形中的比例关系(“蝴蝶定理”:)①S1:S2S4:S3或者 S1S3S2S4②AO:OCS1S2:S4S3蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。梯形中比例关系(“梯形蝴蝶定理”)a22①S1:S3a:b22②S]:S3:S2:S4a:b:ab:ab;③ 梯形 S 的对应份数为 ab2。0.15 倍,黄色三角形的面积是四、相似模型相似三角形性质:②22s^ADE:ABCAF2:AG2所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方。五、燕尾定理模型SAABG:SAAGCSABGE:SAEGCBE:ECSABGASABGCSAAGFSAFGCAF:FC»AGC:»BCG»ADG:S^DGBAD:DB典型例题精讲例 1 一个长方形分成 4 个不同的三角形,绿色三角形面积是长方形面积的①ADAEDEAFABACBCAG21 平方厘米。问:长方形的面积是平方厘米。乍方例 1 图举一反三】两条线段把三角形分为三个三角形和一个四边形,如图所示7,7,贝阴影四边形的面积是多少?三个三角形的面积分别是 3,例 2 如图,三角形田地中有两条小路 AE 和 CF,交叉处为 D,张大伯常走这两条小路,他知道 DF 二 DC,且 AD 二 2DE。贝 IJ 两块地 ACF 和 CFB 的面积比是举一反三图拓展】如图,已知长方形 ADEF 的面积 16,三角形 ADB 的面积是 3,三角形 ACF 的面积是 4,那么三角形 ABC 的面积是多少?拓展图77ARD例 3 图如图,在△ABC 中,已知 M、N 分别...