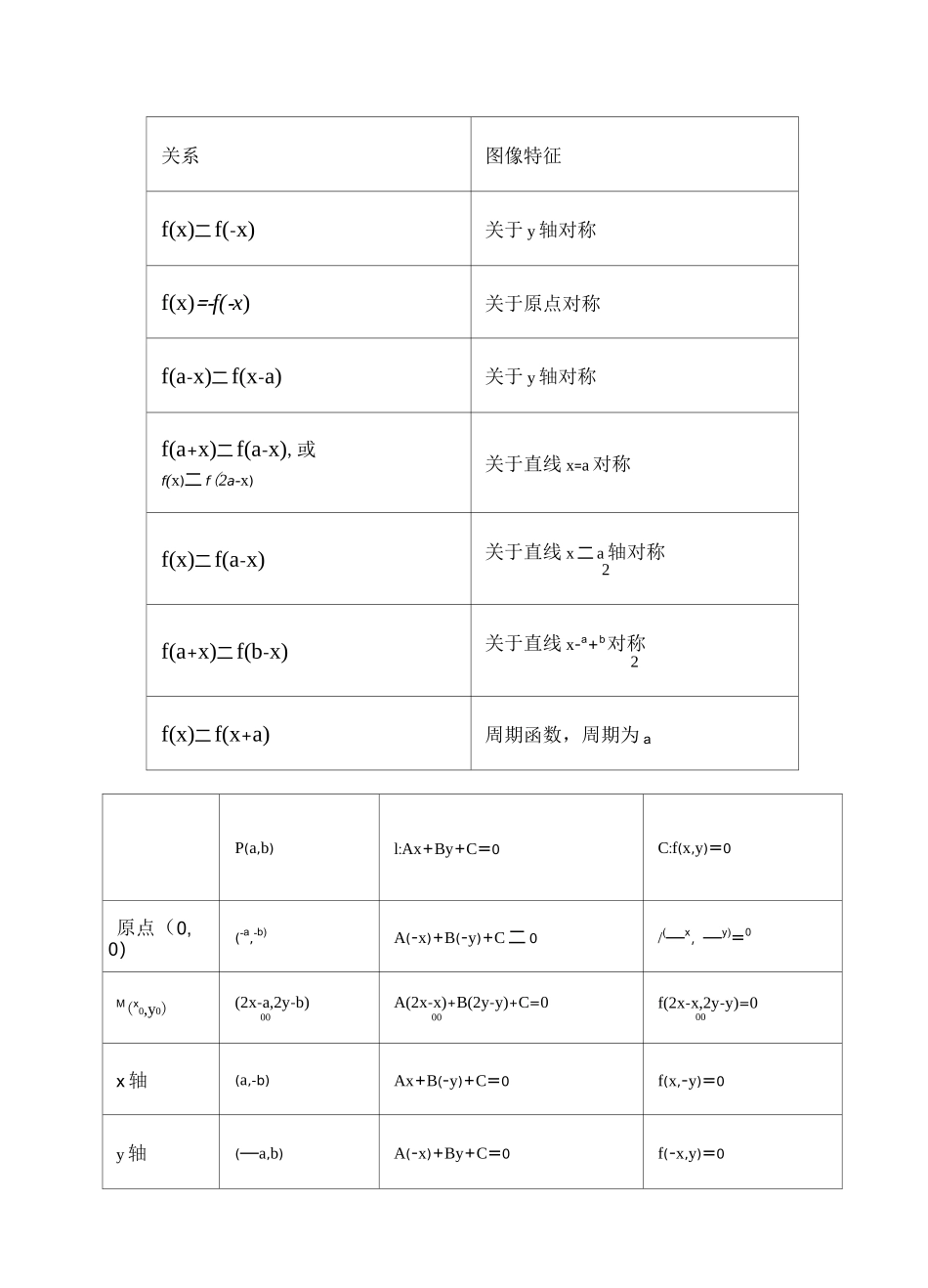
对称性与周期性函数对称性、周期性的判断1. 函数 y=f(x)有 f(a+x)=f(b-x)(若等式两端的两自变量相加为常数,如(a+x)+(b-x)=a+b),则f(x)的图像关于 x=a+b 轴对称;当 a 二 b 时,若2f(a+x)=f(a-x)(或 f(x)=f(2a-x)),则 f(x)关于 x=a 轴对称;2. 函数 y=f(x)有 f(x+a)=f(x-b)(若等式两端的两自变量相减为常数,如(x+a)-(x-b)=a+b),则 f(x)是周期函数,其周期 T=a+b;当 a=b时,若 f(x+a)=f(x-a),则 f(x)是周期函数,其周期T=2a;3. 函数 y=f(x)的图像关于点 P(a,b)对称Of(x)+f(2a-x)=2b(或 f(x)=2b-f(2a-x));函数 y=f(x)的图像关于点 P(a,0)对称 Of(x)=-f(2a-x)(或 f(a+x)=-f(a-x));4. 奇函数 y=f(x)的图像关于点 P(a,0)对称 Oy=f(x)是周期函数,且 T=2a 是函数的一个周期;偶函数 y=f(x)的图像关于点 P(a,0)对称 Oy=f(x)是周期函数,且 T=4a 是函数的一个周期;5. 奇函数 y=f(x)的图像关于直线 x=a 对称 Oy=f(x)是周期函数,且 T=4a 是函数的一个周期;偶函数 y=f(x)的图像关于直线 x=a 对称 Oy=f(x)是周期函数,且 T=2a 是函数的一个周期;6. 函数 y=f(x)的图像关于点 M(a,0)和点 N(b,0)对称 O 函数 y=f(x)是周期函数,且 T=2(a-b)是函数的一个周期;7. 函数 y=f(x)的图像关于直线 x=a 和直线 x=b 对称 O 函数 y=f(x)是周期函数,且 T=2(a-b)是函数的一个周期。关系图像特征f(x)二f(-x)关于 y 轴对称f(x)=-f(-x)关于原点对称f(a-x)二f(x-a)关于 y 轴对称f(a+x)二f(a-x),或f(x)二 f(2a-x)关于直线 x=a 对称f(x)二f(a-x)关于直线 x 二 a 轴对称2f(a+x)二f(b-x)关于直线 x-a+b对称2f(x)二f(x+a)周期函数,周期为 aP(a,b)l:Ax+By+C=0C:f(x,y)=0原点(0,0)(-a,-b)A(-x)+B(-y)+C 二 0/(—x,—y)=0M(x0,y0)(2x-a,2y-b)00A(2x-x)+B(2y-y)+C=000f(2x-x,2y-y)=000x 轴(a,-b)Ax+B(-y)+C=0f(x,-y)=0y 轴(—a,b)A(-x)+By+C=0f(-x,y)=0直线直线x+y+x—y+中心对称问题(点对称问题)直线关于点的对称曲线关于点的对称对称问题\r[点关于直线的对称轴对称问题(线对称问题)直线关于直线的对称曲线关于直线的对称JJ一、点对称(1)点关于点的对称点问题若点 A(x,y),B(x,y),则线段 AB 中点 M 的坐标是(x i + x 2 ,y i + y 2 );据此112222可以解求点与点的中心对称,即求点 M(x,y)关于点 P(a,b)的对称点 M'的坐标 00(x,y),利用中点坐标公式可得 a==b=...