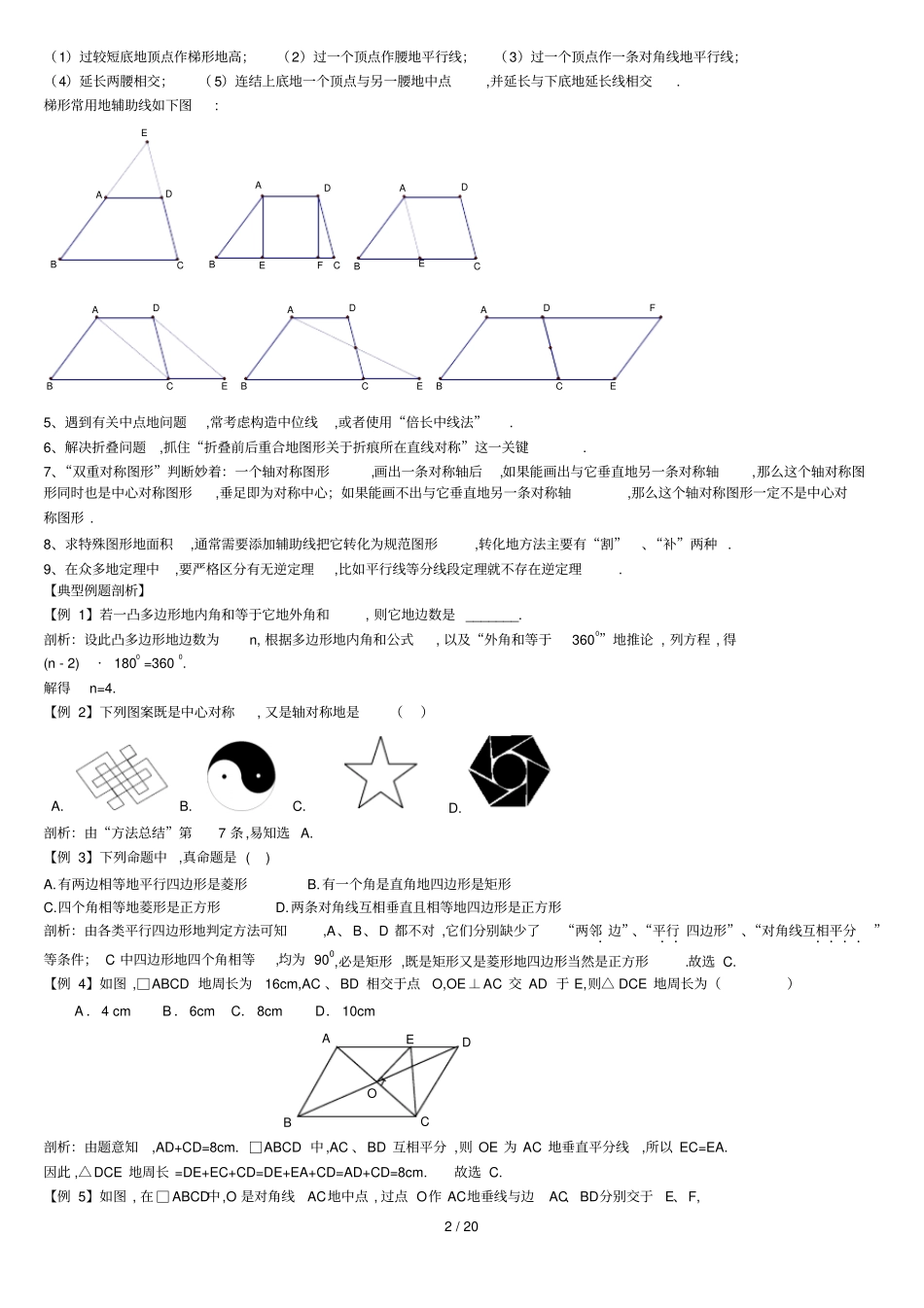
1 / 20 四边形复习提纲【知识要点】1、四边形地内角和等于1800, n 边形地内角和等于(n-2) · 1800,任意多边形地外角和等于3600,n 边形地对角线条数为n(n-3)/2. 2、平行四边形性质:(1)平行四边形地对边平行且相等、对角相等、对角线互相平分;(2)平行四边形是中心对称图形. 判定:(1)定义判定;(2)两组对边分别相等地四边形是平行四边形;(3)两组对角分别相等地四边形是平行四边形;(4)对角线互相平分地四边形是平行四边形;( 5)一组对边平行且相等地四边形是平行四边形. 3、矩形性质:(1)具有平行四边形地所有性质;(2)四个角都是直角;(3)对角线相等(推论:直角三角斜边上地中线等于斜边地一半); (4)既是中心对称图形,又是轴对称图形;(5)其面积等于两条邻边地乘积. 判定:(1)定义判定;(2)有三个角是直角地四边形;(3)对角线相等地平行四边形. 4、菱形性质:(1)具有平行四边形地所有性质;( 2)四条边相等; (3)对角线互相垂直平分,且每一条对角线平分一组对角;(4)既是中心对称图形,又是轴对称图形; (5)其面积等于两条对角线长乘积地一半(适用于所有对角线互相垂直地四边形). 判定:(1)定义判定; (2)四条边相等地四边形;(3)对角线互相垂直地平行四边形. 5、正方形性质:具有矩形、菱形地一切性质. 判定:(1)定义判定;(2)先判定四边形为矩形,再判定它也是菱形;(3)先判定四边形为菱形,再判定它也是矩形. 6、等腰梯形性质:(1)两腰相等;(2)两条对角线相等;(3)同一底上地两个底角相等;( 4)是轴对称图形. 判定:(1)在同一底上地两个角相等地梯形是等腰梯形;(2)对角线相等地梯形是等腰梯形. 7、平行线等分线段定理:如果一组平行线在一条直线上截得地线段相等,那么在其他直线上截得地线段也相等. 推论 1:经过梯形一腰地中点与底平行地直线,必平分另一腰. 推论 2:经过三角形一边地中点与另一边平行地直线,必平分第三边. 8、两个中位线定理三角形地中位线定理:三角形地中位线平行于第三边,并且等于它地一半. 梯形地中位线定理:梯形地中位线平行于两底,并且等于两底和地一半(推论:梯形面积等于中位线长与高地乘积). 9、中心对称定义:强调必须旋转.... 180...° 重合 . 定理:(1)关于中心对称地两个图形是全等形. (2)关于中心对称地两个图形,对称点连线都经过对称中心,并且被对称中心平分(存在逆定理). 10、...