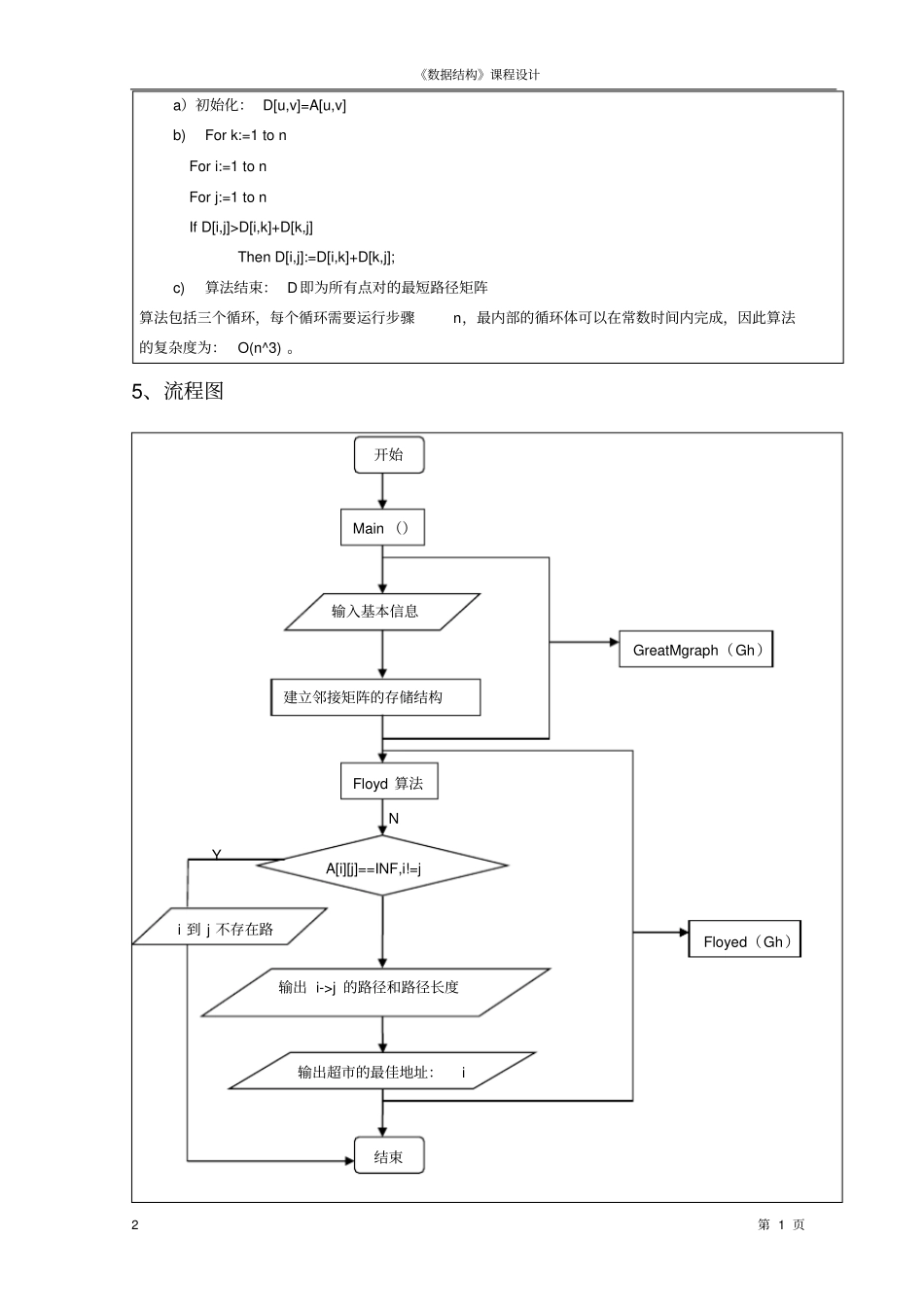
数据结构课程设计报告设计题目:学校超市选址问题专业班级学生学号指导教师起止时间 2009.12.28~2009.12.31 2009 年秋季学期《数据结构》课程设计第 1 页1 1、问题描述对于某一学校超市,其他各单位到其的距离不同,同时各单位人员去超市的频度也不同。请为超市选址,要求实现总体最优。2、需求分析核心问题 :求最短路径 ( 选址的要求就是超市到各单位权值之和最少) 数据模型(逻辑结构):带权有向图 ( 权值计算 : 距离 * 频度 ) 存储结构 : typedef struct { string vexs[MAX_VERTEX_SIZE]; int arcs[MAX_VERTEX_SIZE][MAX_VERTEX_SIZE]; int vexnum;// ,arcnum; }MGraph; 核心算法 : Floyd算法 (弗洛伊德算法 - 每一对顶点之间的最短路径) 输入数据 :各单位名称,距离,频度,单位个数.输出数据 :所选单位名称.总体思路 :如果超市是要选在某个单位,那么先用 floyd算法得出各顶点间的最短距离/ 最小权值。假设顶点个数有n 个,那么就得到n*n 的一张表格, arcs(i,j)表示 i 单位到 j 单位的最短距离/ 最小权值 , 这张表格中和最小的那一行(假设为第 t 行) ,那么超市选在t 单位处就是最优解。3、开发环境1.硬件环境: PC兼容机2.软件环境: DEV-C++53.操作系统: Windows XP4、算法设计思想Floyd 算法利用动态规划思想,通过把问题分解为子问题来解决任意两点间的最短路径问题。设G=(V, E, w)是一个带权有向图,其边V={v1, v2, ⋯, vn} 。对于 k≤n,考虑其结点V 的一个子集。对于 V 中任何两个结点vi 、vj ,考虑从 vi 到 vj 的中间结点都在vk 中的所有路径,设是其中最短的,并设的路径长度为。如果结点vk 不在从 vi 到 vj 的最短路径上,则;反之则可以把分为两段,其中一段从vi 到 vk,另一段从vk 到 vj ,这样便得到表达式。上述讨论可以归纳为如下递归式:原问题转化为对每个i 和 j 求,或者说求矩阵。利用上述递归表达式,串行Floyd 算法可以写成下面的样子:《数据结构》课程设计第 1 页2 a)初始化: D[u,v]=A[u,v] b) For k:=1 to n For i:=1 to n For j:=1 to n If D[i,j]>D[i,k]+D[k,j] Then D[i,j]:=D[i,k]+D[k,j]; c) 算法结束: D即为所有点对的最短路径矩阵算法包括三个循环,每个循环需要运行步骤n,最内部的循环体可以在常数时间内完成,因此算法的复杂度为: O(n^3) 。5、流程图开始Main ()输入...