公式法一课件VIP免费

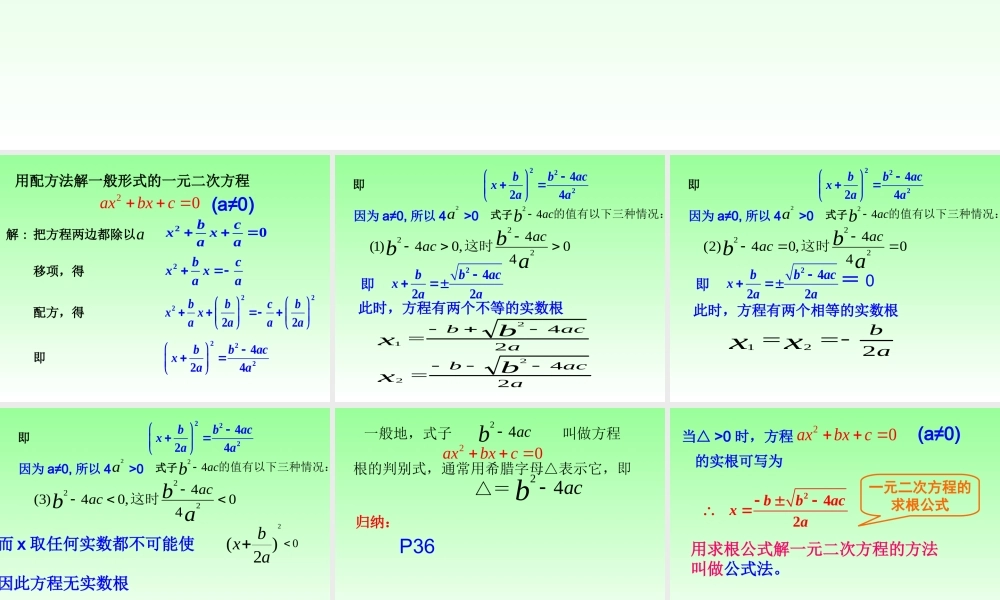
用配方法解一般形式的一元二次方程20axbxc 把方程两边都除以 20bcxxaa解 :a移项，得2bcxxaa配方，得22222bbcbxxaaaa即222424bbacxaa(a≠0) 2422bbacxaa即即222424bbacxaa因为 a≠0, 所以 4 >0a2式子的值有以下三种情况：acb42 044,04)1(222abbacac这时此时，方程有两个不等的实数根aacbaacbbxbx24242221 2422bbacxaa即即222424bbacxaa因为 a≠0, 所以 4 >0a2式子的值有以下三种情况：acb42 044,04)2(222abbacac这时此时，方程有两个相等的实数根abxx221＝ 0 即222424bbacxaa因为 a≠0, 所以 4 >0a2式子的值有以下三种情况：acb42 044,04)3(222abbacac这时而 x 取任何实数都不可能使 ，因此方程无实数根0)2(2 abx 一般地，式子 叫做方程根的判别式，通常用希腊字母△表示它，即△＝acb42 acb42 20axbxc归纳：P36 20axbxc 242bbacxa一元二次方程的求根公式(a≠0)当△ >0 时，方程的实根可写为用求根公式解一元二次方程的方法叫做公式法。 例 1 解方程： 27180xx解：即 ：1292xx242bbacxa1718abc22474 118121bac  （）（ ）>0方程有两个不等的实数根242bbacxa211712121)7( 用公式法解一元二次方程的一般步骤：242bbacxa3 、代入求根公式 :2 、求出 的值，24bac1 、把方程化成一般形式，并写出 的值。a b、、c4 、写出方程的解：12xx、特别注意 : 当 时无解240bac 242bbacxa例 2 解方程：232 3xx化简为一般式：22 330xx这里1a  、 b=- 2 3、 c=3解：2242 34 1 30032 12bacx   （）（- 2 3）2 3即 ：123xx 解：去括号，化简为一般式：242bbacxa例 3 解方程：2136xx23780xx这里3a  、 b=- 7、 c=822474 3 84996470bac -（） 方程没有实数解。 用公式法解下列方程：（ 1 ） 2x2-9x+8=0;（ 2 ） 9x2+6x+1=0;（ 3 ） 16x2+8x=3.随堂随堂练习练习 1 、 m 取什么值时，方程 x2+(2m+1)x+m2-4=0 有两个相等的实数解 思考题2 、关于 x 的一元二次方程 ax2+bx+c=0 (a≠0) 。 当 a ， b ， c 满足什么条件时，方程的两根为互为相反数？ 5作业：P42