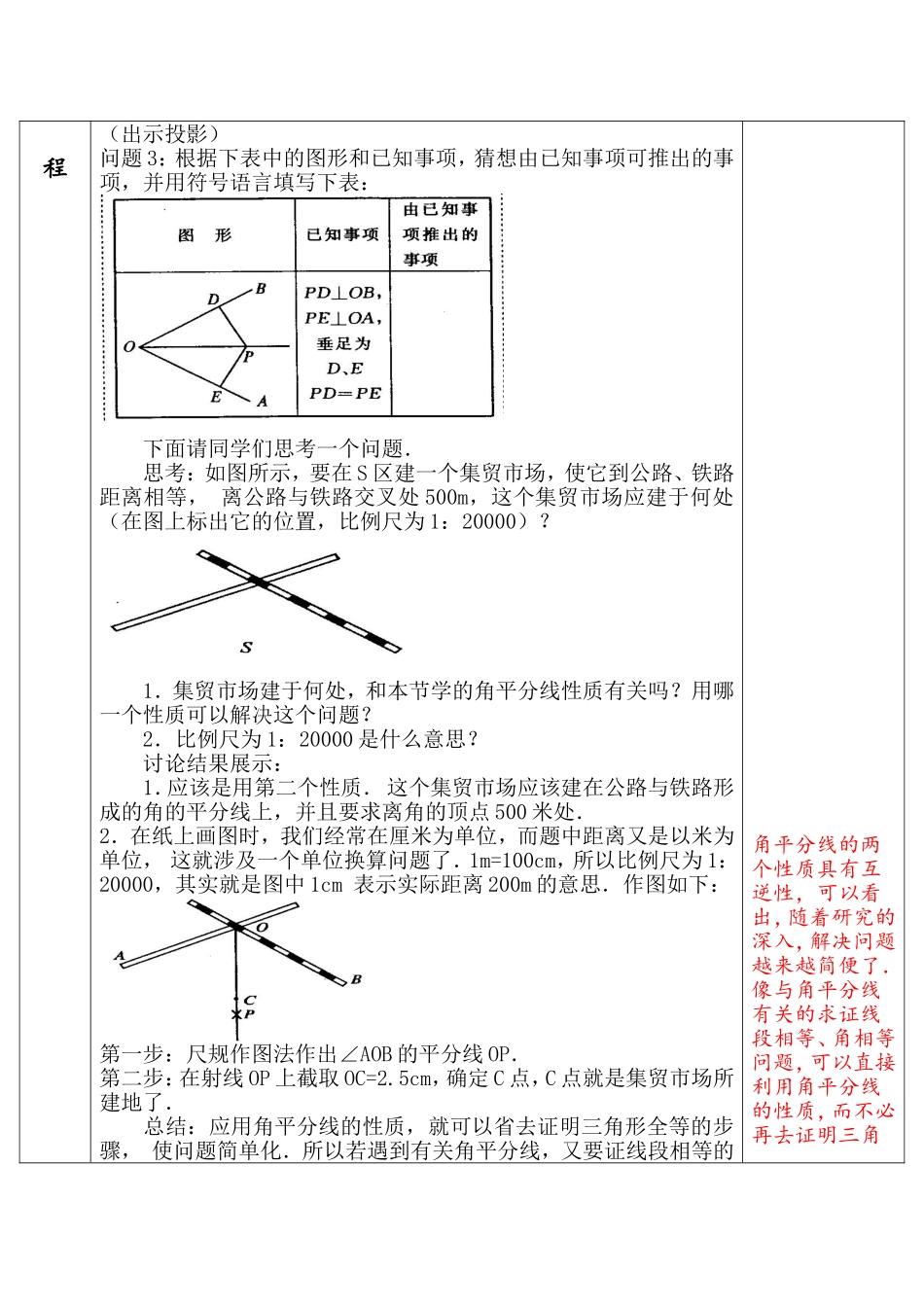
课时总 第( 17 )课时 二次备课课题第十二章 全等三角形 12.3 角平分线的性质(二)授课类型新 授学 习目标知识与技能:1、掌握角的平分线的性质2、会叙述角的平分线的性质及“到角两边距离相等的点在角的平分线上”.过程与方法:能应用这两个性质解决一些简单的实际问题.情感、态度与价值观:通过折纸、画图、文字一符号的翻译活动,培养学生的联想、探索、概括归纳的能力,激发学生学习数学的兴趣. 教学重、难点教学重点:角平分线的性质及其应用.教学难点:灵活应用两个性质解决问题.教学方法小组讨论、活动探究、归纳总结教学手段多媒体一.创设情境,引入新课 [师]请同学们拿出准备好的折纸与剪刀,自己动手,剪一个角,把剪好的角对折,使角的两边叠合在一起,再把纸片展开,你看到了什么?把对折的纸片再任意折一次,然后把纸片展开,又看到了什教学过程教学过么?二.导入新课 角平分线的性质即已知角的平分线,能推出什么样的结论. 操作:1.折出如图所示的折痕 PD、PE.2.你与同伴用三角板检测你们所折的折痕是否符合图示要求. 画一画: 按照折纸的顺序画出一个角的三条折痕,并度量所画 PD、PE 是否等长? 拿出两名同学的画图,放在投影下,请大家评一评,以达明确概念的目的. 问题 1:你能用文字语言叙述所画图形的性质吗? 问题 2:(出示投影片)能否用符号语言来翻译“角平分线上的点到角的两边的距离相等”这句话.请填下表: 学生通过讨论作出下列概括: 已知事项:OC 平分∠AOB,PD⊥OA,PE⊥OB,D、E 为垂足. 由已知事项推出的事项:PD=PE. 于是我们得角的平分线的性质: 在角的平分线上的点到角的两边的距离相等. [师]那么到角的两边距离相等的点是否在角的平分线上呢?应用角平分线的性质,就可以省去证明三角形全等的步骤,使问题简单化.所以若遇到有关角平分线,又要证线段相等的问题,我们可以直接利用性质解决问题程(出示投影)问题 3:根据下表中的图形和已知事项,猜想由已知事项可推出的事项,并用符号语言填写下表: 下面请同学们思考一个问题. 思考:如图所示,要在 S 区建一个集贸市场,使它到公路、铁路距离相等,离公路与铁路交叉处 500m,这个集贸市场应建于何处(在图上标出它的位置,比例尺为 1:20000)? 1.集贸市场建于何处,和本节学的角平分线性质有关吗?用哪一个性质可以解决这个问题? 2.比例尺为 1:20000 是什么意思? 讨论结果展示...