直线的距离公式VIP免费

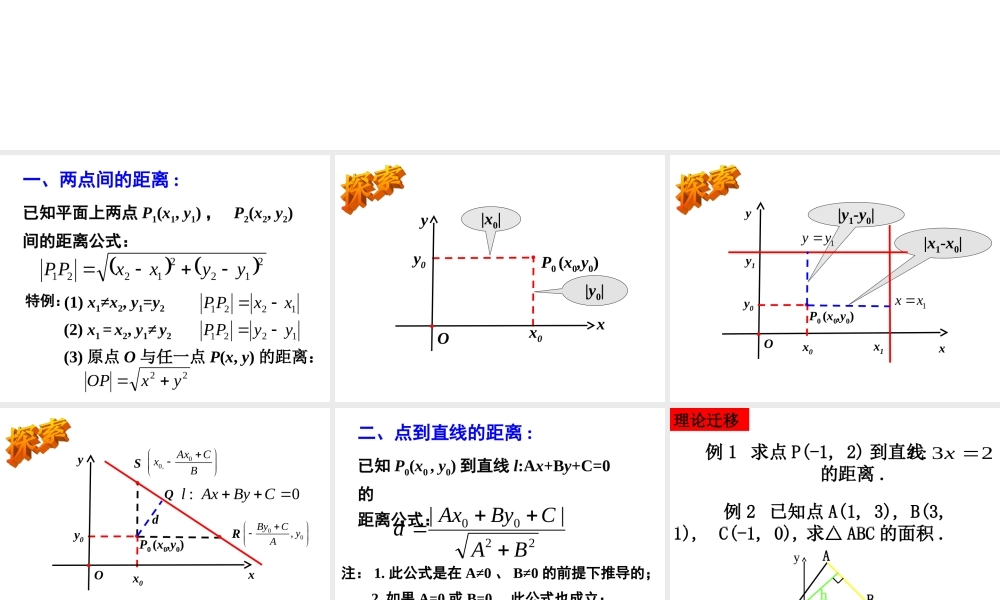
3.3.3 点到直线的距离3.3.4 两条平行直线间的距离 学 . 科 .网 一、两点间的距离 :已知平面上两点 P1(x1, y1) ， P2(x2, y2)间的距离公式：(1) x1≠x2, y1=y2(2) x1 = x2, y1≠ y2特例：1221xxPP1221yyPP(3) 原点 O 与任一点 P(x, y) 的距离：22yxOP21221221yyxxPP xyP0 (x0,y0)O|y0||x0|x0y0 xyP0 (x0,y0)O|x1-x0||y1-y0|x0y01yyy11xxx1 xyP0 (x0,y0)Ox0y0:0lAxByCS00,AxCxBR00,ByC yA001 ||||2 P SP RQd1||2 d SR 2200||BACByAxd注： 1. 此公式是在 A≠0 、 B≠0 的前提下推导的；2. 如果 A=0 或 B=0 ，此公式也成立；3. 用此公式时直线方程要先化成一般式。二、点到直线的距离 :已知 P0(x0 , y0) 到直线 l:Ax+By+C=0的距离公式： 理论迁移 例 1 求点 P(-1, 2) 到直线 的距离 .23:xl 例 2 已知点 A(1, 3), B(3, 1), C(-1, 0), 求△ ABC 的面积 .xyoACBh 知识探究（二）：两平行直线的距离思考 1: 两条平行直线的相对位置关系常通过距离来反映，两平行直线间的距离的含义是什么？ ( 夹在两条平行直线间公垂线的长 ) 思考 2: 你有什么办法求两条平行直线之间的距离？AB Oyxl2l1PQ任意两条平行直线都可以写成如下形式：l1 :Ax+By+C1=0l2 :Ax+By+C2=022200BACByAxd2221BACC2221BACCd(x0,y0) 2221||BACCd三、两条平行直线的距离 :注 :1. 用公式时，直线方程化为一般式 ; 2. 用两平行线间距离公式须将方程中 x 、 y 的系数化为对应相同的形式。两条平行直线 间的距离公式：l1 :Ax+By+C1=0 与l2 :Ax+By+C2=0 例 3 已知直线 和 与 ,l1 与 l2 是否平行？若平行 , 求 l1 与 l2的距离 .0872:1yxl01216:2yxl (1) 2x+3y-8=0 ， 2x+3y+18=0(2) 3x+4y=10 ， 6x+8y-10=0132132632|)8(18|22d143|)10(5|22d求下列两条平行线的距离： 【总一总★成竹在胸】2. 两条平行线 Ax+By+C1=0 与 Ax+By+C2=0 的距离1. 平面内一点 P(x0,y0) 到直线 Ax+By+C=0 的距离当 A=0 或 B=0 时 , 公式仍然成立 .1222 .CCdAB2200BACByAxd