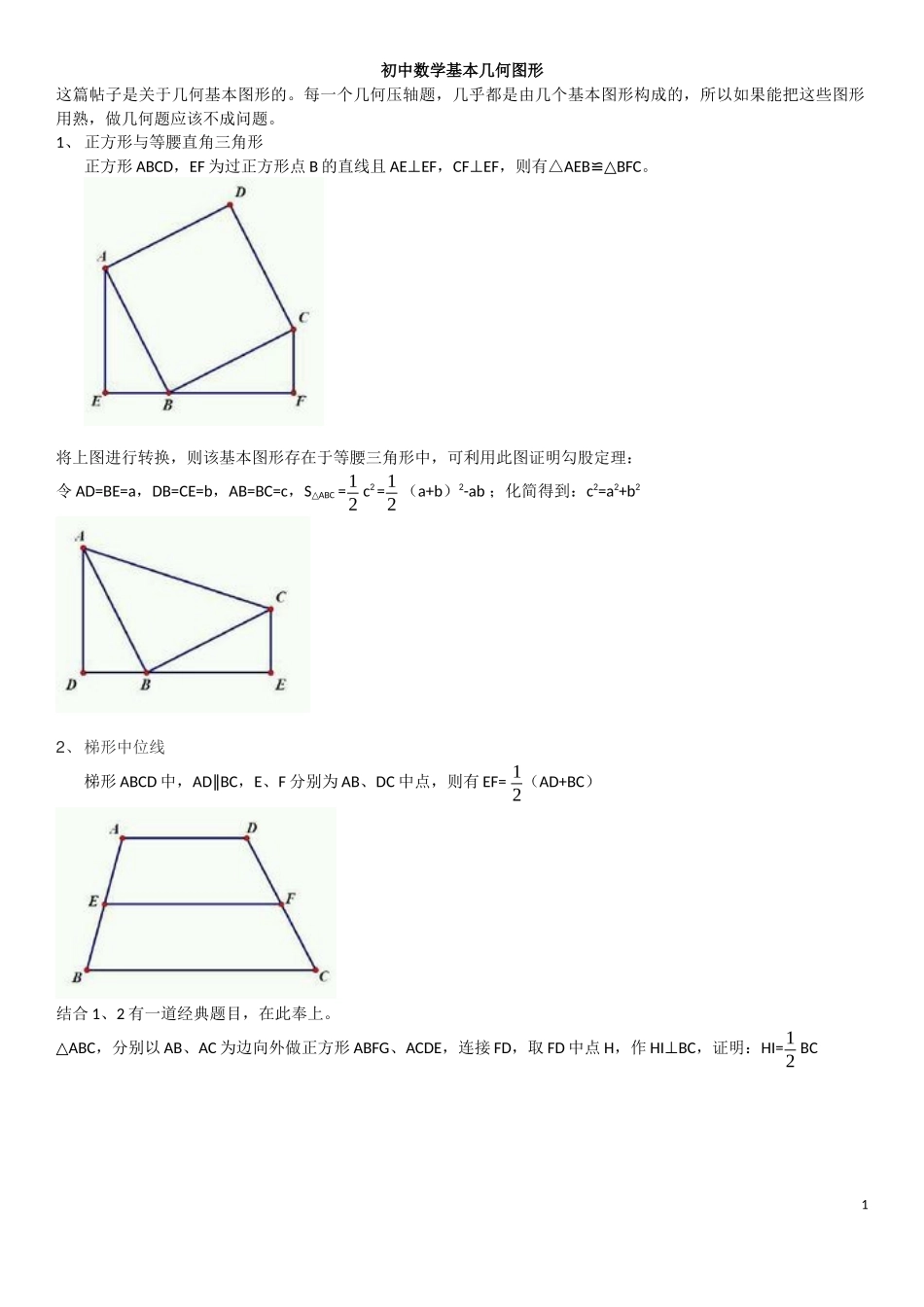
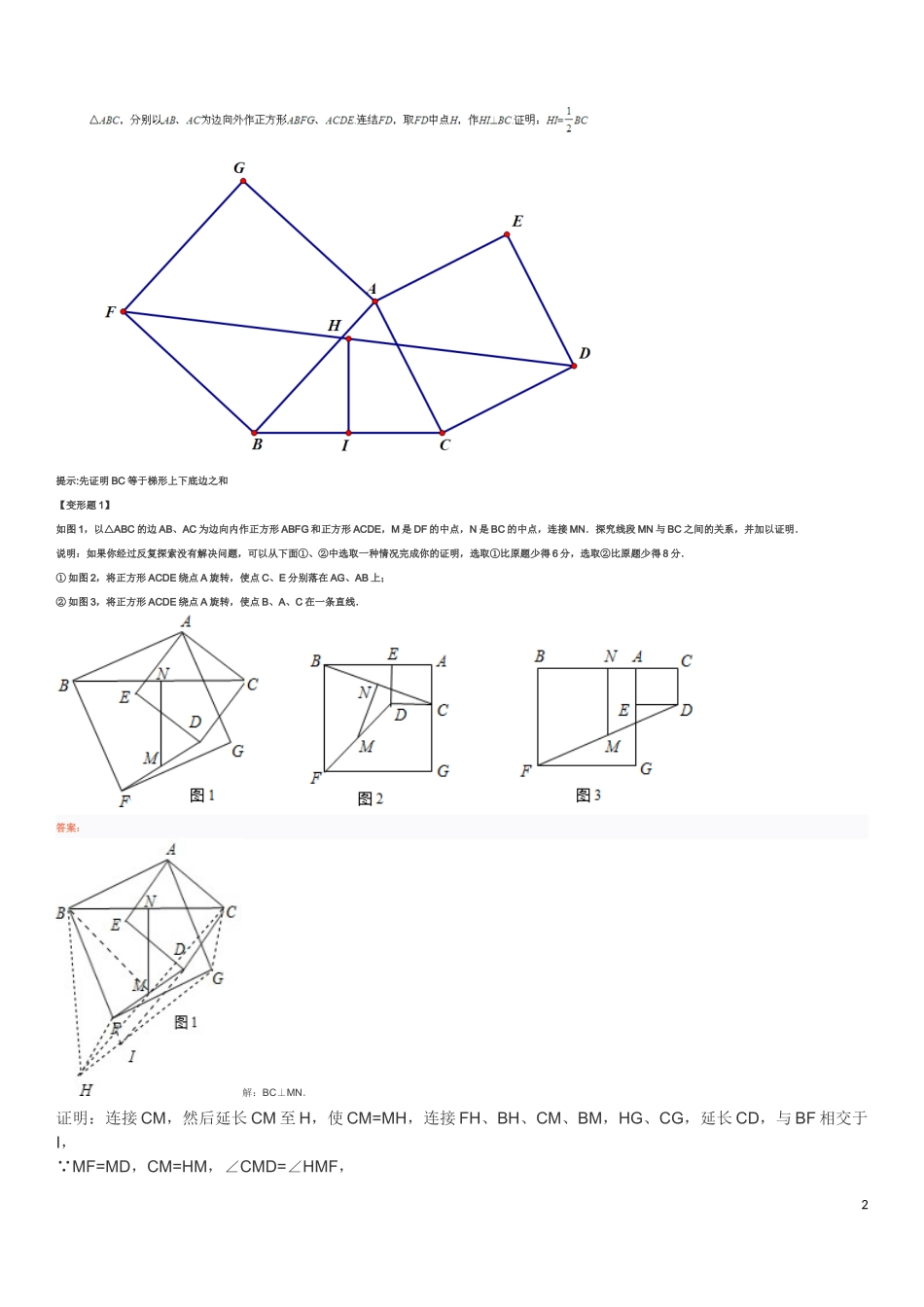
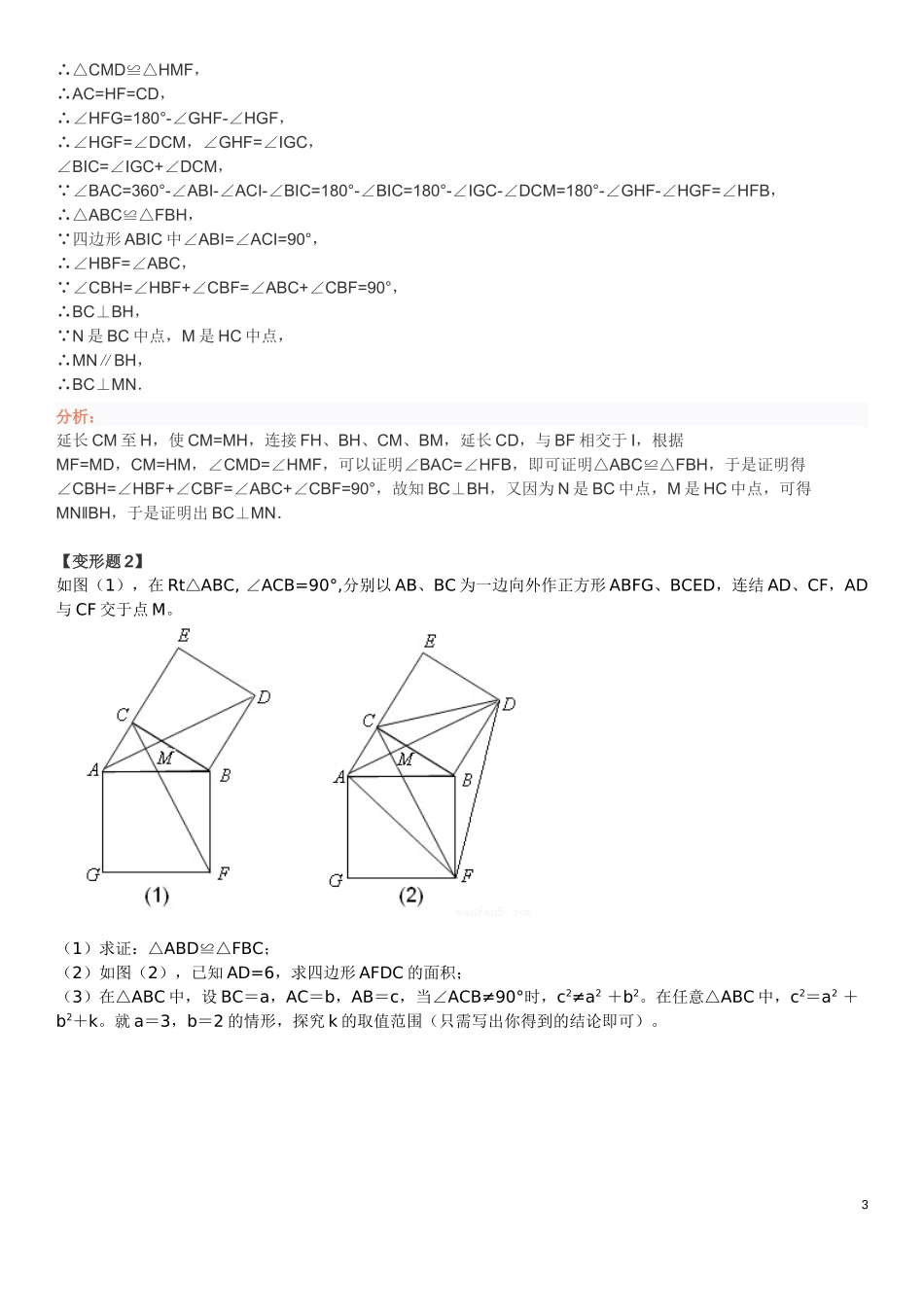
初中数学基本几何图形这篇帖子是关于几何基本图形的。每一个几何压轴题,几乎都是由几个基本图形构成的,所以如果能把这些图形用熟,做几何题应该不成问题。1、正方形与等腰直角三角形正方形ABCD,EF为过正方形点B的直线且AEEF⊥,CFEF⊥,则有△AEBBFC≌△。将上图进行转换,则该基本图形存在于等腰三角形中,可利用此图证明勾股定理:令AD=BE=a,DB=CE=b,AB=BC=c,SABC△=12c2=12(a+b)2-ab;化简得到:c2=a2+b22、梯形中位线梯形ABCD中,ADBC∥,E、F分别为AB、DC中点,则有EF=12(AD+BC)结合1、2有一道经典题目,在此奉上。ABC△,分别以AB、AC为边向外做正方形ABFG、ACDE,连接FD,取FD中点H,作HIBC⊥,证明:HI=12BC1提示:先证明BC等于梯形上下底边之和【变形题1】如图1,以△ABC的边AB、AC为边向内作正方形ABFG和正方形ACDE,M是DF的中点,N是BC的中点,连接MN.探究线段MN与BC之间的关系,并加以证明.说明:如果你经过反复探索没有解决问题,可以从下面①、②中选取一种情况完成你的证明,选取①比原题少得6分,选取②比原题少得8分.①如图2,将正方形ACDE绕点A旋转,使点C、E分别落在AG、AB上;②如图3,将正方形ACDE绕点A旋转,使点B、A、C在一条直线.答案:解:BC⊥MN.证明:连接CM,然后延长CM至H,使CM=MH,连接FH、BH、CM、BM,HG、CG,延长CD,与BF相交于I,∵MF=MD,CM=HM,∠CMD=∠HMF,2∴△CMD≌△HMF,∴AC=HF=CD,∴∠HFG=180°-∠GHF-∠HGF,∴∠HGF=∠DCM,∠GHF=∠IGC,∠BIC=∠IGC+∠DCM,∵∠BAC=360°-∠ABI-∠ACI-∠BIC=180°-∠BIC=180°-∠IGC-∠DCM=180°-∠GHF-∠HGF=∠HFB,∴△ABC≌△FBH,∵四边形ABIC中∠ABI=∠ACI=90°,∴∠HBF=∠ABC,∵∠CBH=∠HBF+∠CBF=∠ABC+∠CBF=90°,∴BC⊥BH,∵N是BC中点,M是HC中点,∴MN∥BH,∴BC⊥MN.分析:延长CM至H,使CM=MH,连接FH、BH、CM、BM,延长CD,与BF相交于I,根据MF=MD,CM=HM,∠CMD=∠HMF,可以证明∠BAC=∠HFB,即可证明△ABC≌△FBH,于是证明得∠CBH=∠HBF+∠CBF=∠ABC+∠CBF=90°,故知BC⊥BH,又因为N是BC中点,M是HC中点,可得MNBH‖,于是证明出BC⊥MN.【变形题2】如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M。(1)求证:△ABD≌△FBC;(2)如图(2),已知AD=6,求四边形AFDC的面积;(3)在△ABC中,设BC=a,AC=b,AB=c,当∠ACB≠90°时,c2≠a2+b2。在任意△ABC中,c2=a2+b2+k。就a=3,b=2的情形,探究k的取值范围(只需写出你得到的结论即可)。3【变形题3】已知:如图所示,从RtABC△的两直角边AB,AC向外作正方形ABFG及ACDE,CF,BD分别交AB,AC于P,Q.求证:AP=AQ.43、角平分线出等腰。AD平分∠BAC,且BD∥AC,则BA=BD,此图形常出现于菱形中,若有AB=AC,则连接CD后有菱形BACD。补充一句,上一图可用于证明角分线定理。4、双垂图。55、一线三等角相似AB=AC,∠ADE=∠B,则△ABDDCE∽△6、正方形中两垂直线段。正方形ABCD中,AF⊥DE,则有AF=DE;平移AF、DE进行推广,在正方形ABCD中,MN⊥PQ,则有MN=PQ7、直角三角形斜边中线。AB⊥AC,D为BC中点,则AD=BD=CD,该图可从矩形中挖出,也可从圆中找到图形。68、直角三角形共圆9、等腰三角形线段关系711、常见旋转型2。812、常见旋转型313、四边形共圆9四边形共圆2一道经典例题一线三角模型的特殊形式。10补充:一线三角相等模型中,∠B=∠C=∠ADE=n°,则∠ADB+∠EDC=180-n°,∠DEC+∠EDC=180-n°所以,∠ADB=∠DEC,又因为∠B=∠C,所以△ADB相似于△DEC,所以AD/DE=BD/CE。当点D为中点时,BD=DC,则AD/DE=DC/CE,又因为∠C=∠ADE,所以△ADE相似于△DEC。证毕双等边三角形(正方形)模型上一楼图形的性质性质1:通过证全等可知左图中,BD=AE,右图中,BE=DF性质2:证全等后,做双高可知左图中,CF平分∠BFE,右图中,CH平分∠BHF性质3:左图中,BD和AE相交所构成的其中的一个角为60°,右图中,BE和DF垂直,当扩展到正n边形时,两线相交所构成的其中的一个角等于这个正n边形的各个内角。北京中考经典好题。1112