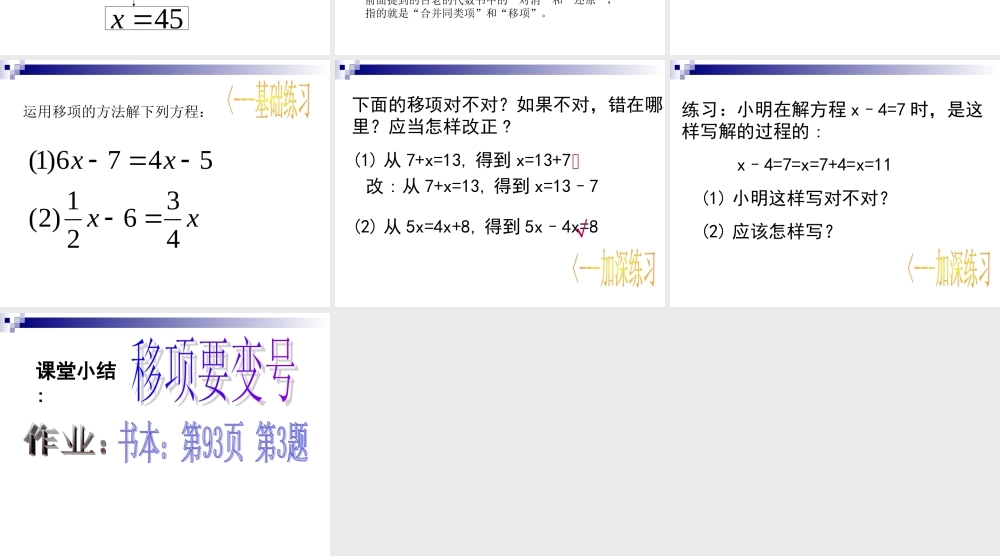
问题 把一些图书分给某班学生阅读,如果每人分 3 本,则剩余 20 本,如果每人分 4 本,则还缺 25 本。这个班有多少人? 设这个班有 x 名学生。 每人分 3 本,共分出 ___ 本,加上剩余的 20 本,这批书共 ________ 本。 每人分 4 本,需要 _____ 本,减去缺的 25 本,这批书共 _________ 本。254203xx203 x这批书的总数是一个定值,表示它的两个式子应相等,即表示同一个量的两个不同的式子相等。根据这一相等关系列得方程:这批书的总数有几种表示法?它们之间的关系有什么关系?本题哪个相等关系可作为列方程的依据呢?x4x3254 x 方程的两边都有含 x 的项( 3x 和 4x )和不含字母的常数项( 20 与- 25 ),怎样才能使它向 x=a (常数)的形式转化呢?254203xx 检验:方程的两边都代入x=12, 得 左边 =12–7=5, 右边 =5 左边 =右边 所以 x=12 是原方程的解。 x – 7 = 5解 1 :方程两边都加7, 得 x –7+7=5+7 x=5+7 x=12x –7 = 5 x = 5 +7 x = 12从左移右改变符号检验:方程的两边都代入x=12, 得 左边 =12–7=5, 右边 =5, 左边 = 右边 所以 x=12 是原方程的解。 解 2 :像上面这样把等式一边的某项变号后移到另一边,叫做 移项 。 254203xx202543xx45 x45x移项合并同类项系数化为 1 上面解方程中“移项”起到了什么作用?作用:把同类项移到等式的某一边, 以进行合并。 解方程时经常要“合并同类项”和“移项”,前面提到的古老的代数书中的“对消”和“还原”,指的就是“合并同类项”和“移项”。 解方程:xx23273解:移项,得合并同类项,得系数化为 1 ,得73223 xx255 x5x 运用移项的方法解下列方程:xxxx43621)2(5476)1( 下面的移项对不对?如果不对,错在哪里?应当怎样改正 ?(1) 从 7+x=13, 得到 x=13+7(2) 从 5x=4x+8, 得到 5x–4x=8 改 : 从 7+x=13, 得到 x=13–7 练习:小明在解方程 x–4=7 时,是这样写解的过程的 : x–4=7=x=7+4=x=11 (1) 小明这样写对不对? (2) 应该怎样写? 课堂小结: