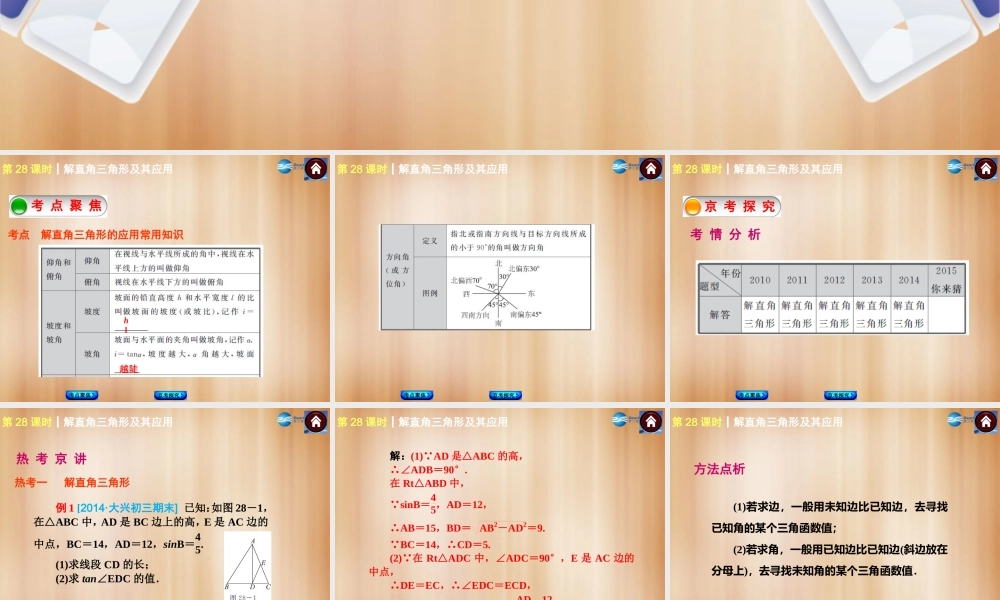
第 28 课时 解直角三角形及其应用京 考 探 究京 考 探 究考 点 聚 焦考 点 聚 焦考 点 聚 焦考点 解直角三角形的应用常用知识考点聚焦京考探究第 28 课时┃解直角三角形及其应用hl 越陡第 28 课时┃解直角三角形及其应用考点聚焦京考探究 考 情 分 析京 考 探 究第 28 课时┃解直角三角形及其应用考点聚焦京考探究热考一 解直角三角形热 考 京 讲第 28 课时┃解直角三角形及其应用例 1 [2014·大兴初三期末] 已知:如图 28-1,在△ABC 中,AD 是 BC 边上的高,E 是 AC 边的中点,BC=14,AD=12,sinB=45. (1)求线段 CD 的长; (2)求 tan∠EDC 的值. 考点聚焦京考探究第 28 课时┃解直角三角形及其应用解:(1) AD 是△ABC 的高, ∴∠ADB=90°. 在 Rt△ABD 中, sinB=45,AD=12, ∴AB=15,BD= AB2-AD2=9. BC=14,∴CD=5. (2) 在 Rt△ADC 中,∠ADC=90°,E 是 AC 边的中点, ∴DE=EC,∴∠EDC=ECD, ∴tan∠EDC=tan∠ECD=ADCD=125 . 考点聚焦京考探究 方法点析第 28 课时┃解直角三角形及其应用(1)若求边,一般用未知边比已知边,去寻找已知角的某个三角函数值; (2)若求角,一般用已知边比已知边(斜边放在分母上),去寻找未知角的某个三角函数值. 考点聚焦京考探究热考二 解有关高度 ( 宽度 ) 的问题第 28 课时┃解直角三角形及其应用例 2 [2014·西城初三期末] 如图 28-2,为了估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点 B,C,D,使得 AB⊥BD,∠ACB=45°,∠ADB=30°,并且点 B,C,D在同一条直线上.若测得 CD=30 米,求河宽AB.(结果精确到 1 米, 3取 1.73, 2取 1.41) 考点聚焦京考探究第 28 课时┃解直角三角形及其应用解:设河宽 AB 为 x 米. AB⊥BC, ∴∠ABC=90°. 在 Rt△ABC 中,∠ACB=45°, ∴AB=BC=x. 在 Rt△ABD 中,∠ADB=30°, ∴BD= 3AB= 3x. ∴CD=BD-BC= 3x-x=30. 解得 x=15 3+15≈41. 答:河宽 AB 约为 41 米. 考点聚焦京考探究第 28 课时┃解直角三角形及其应用 结合视角知识构造直角三角形 在实际测量高度、宽度、距离等问题中,常结合视角知识构造直角三角形,利用三角函数或相似三角形来解决问题.常见的构造的基本图形有如下几种: (1)不同地点看同一点; (2)同一地点看不同点; (3)利用反射构...