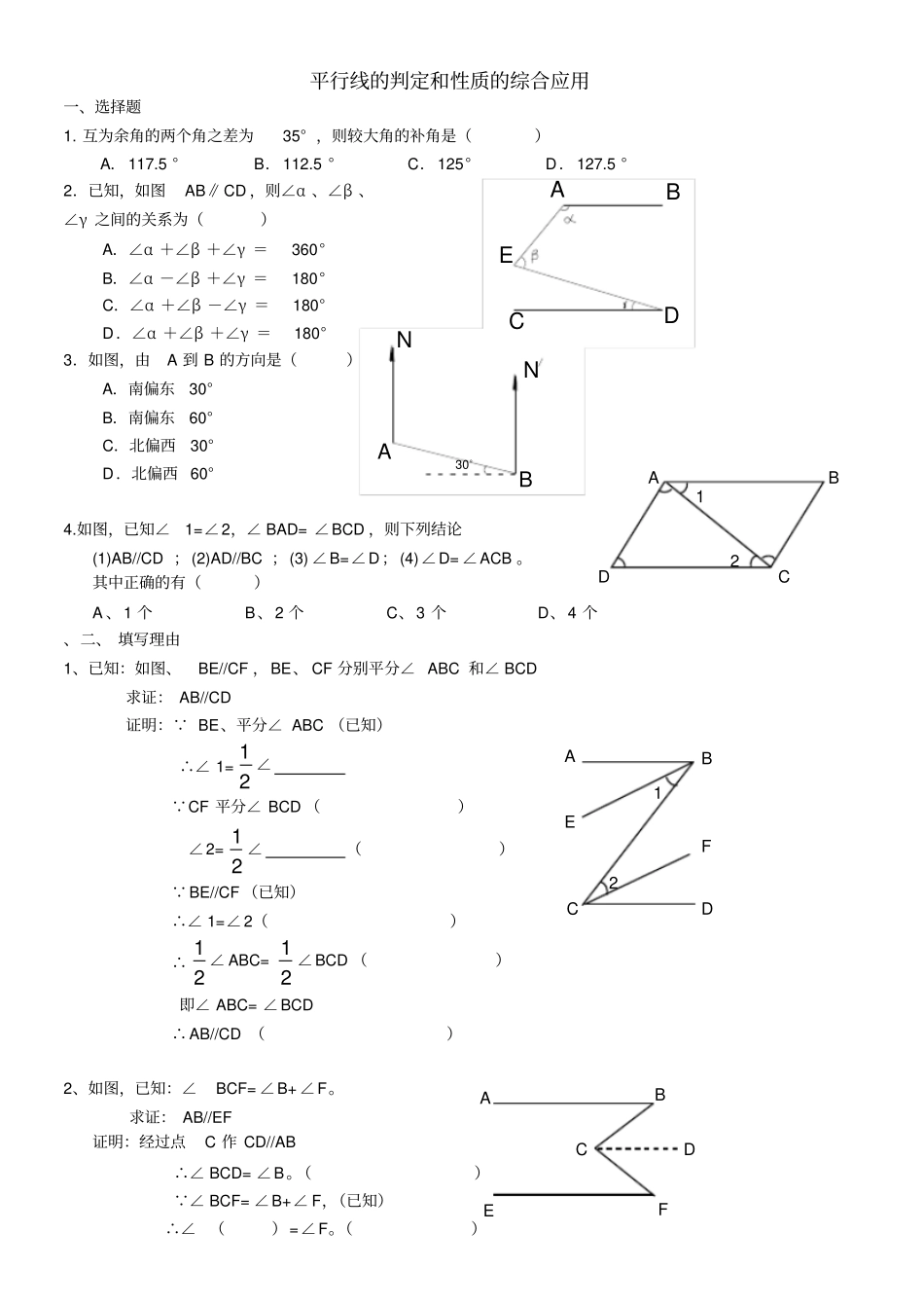
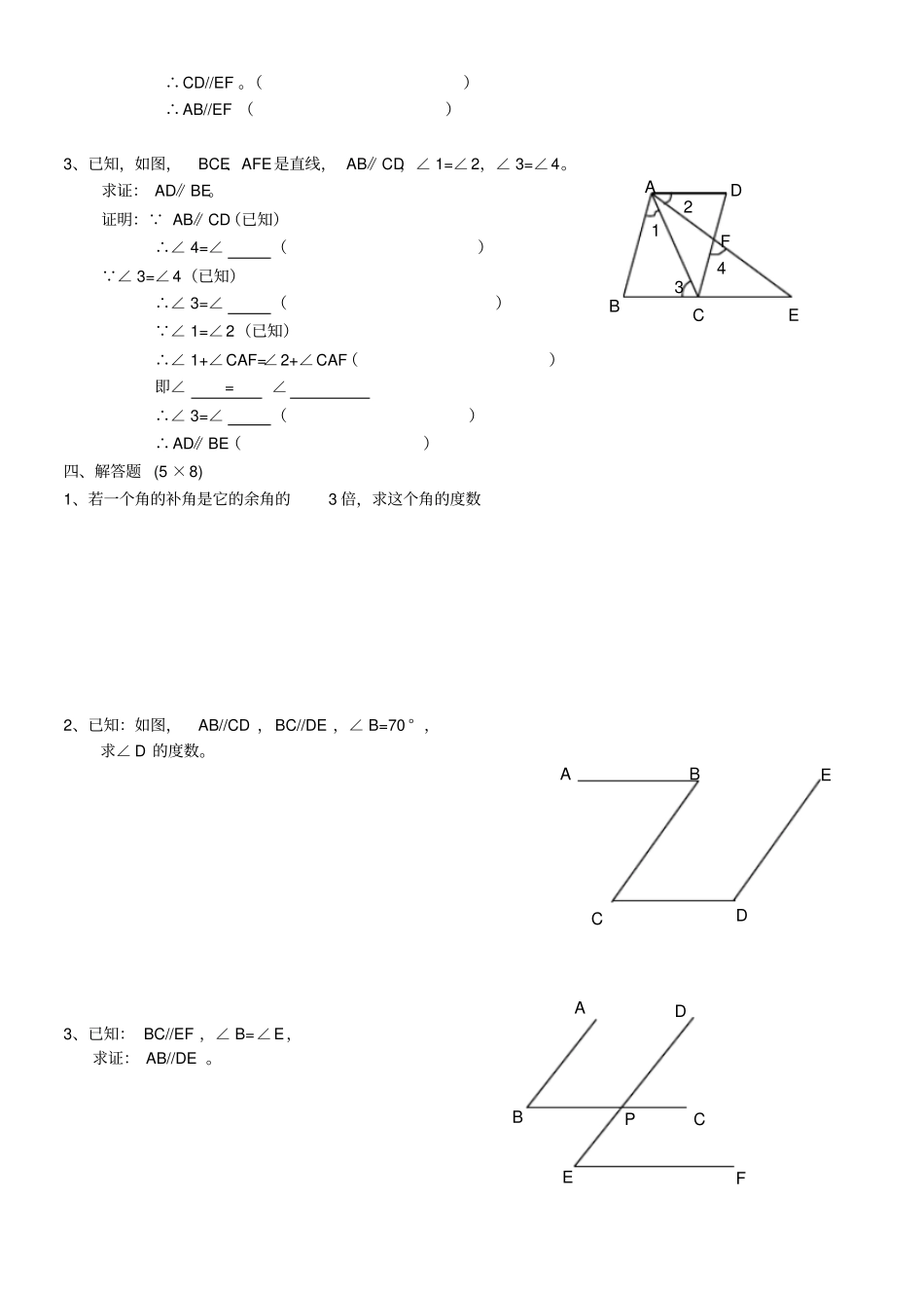
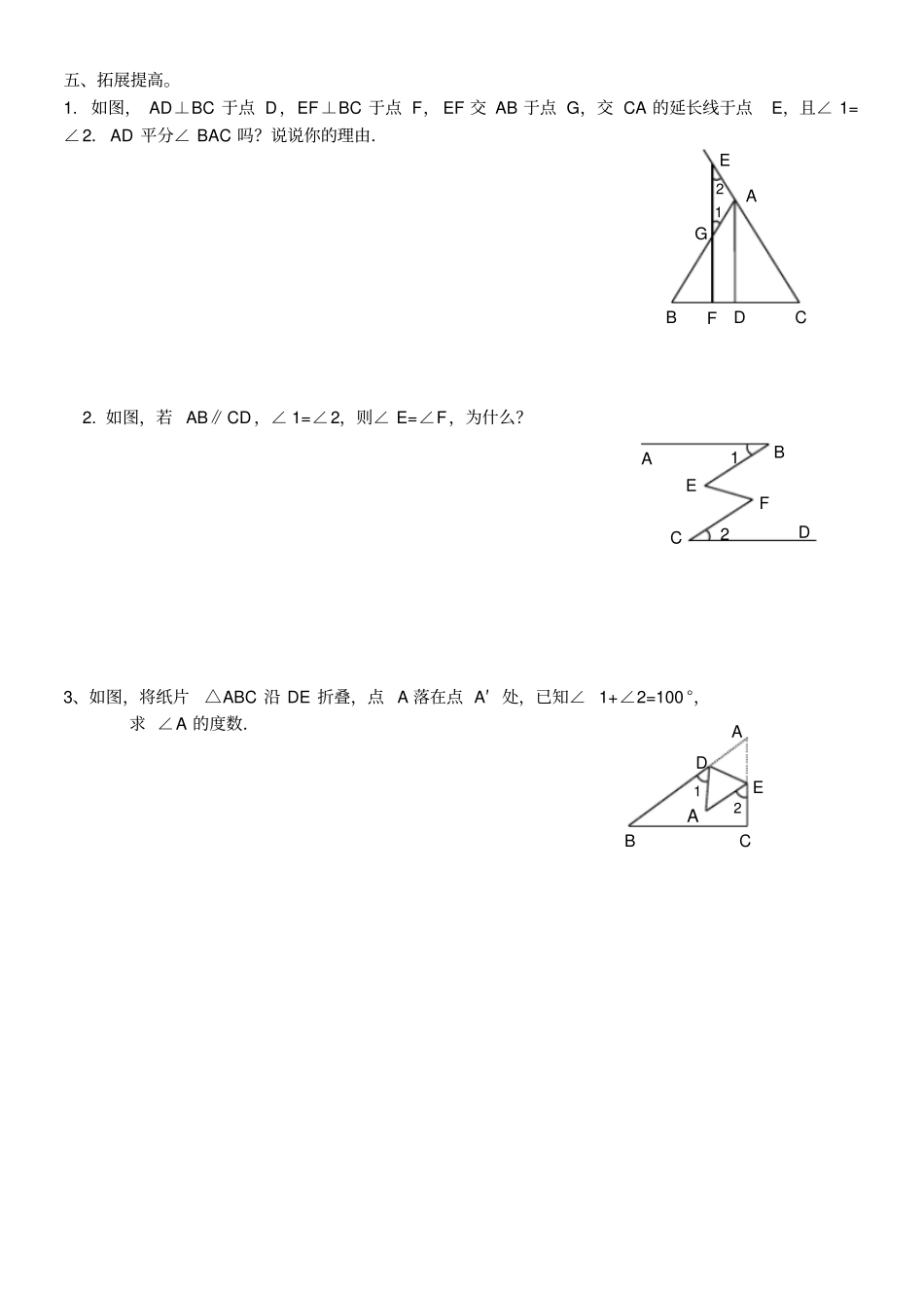
平行线的判定和性质的综合应用一、选择题1. 互为余角的两个角之差为35° ,则较大角的补角是()A.117.5 °B.112.5 °C.125°D.127.5 °2.已知,如图AB∥CD ,则∠α 、∠β 、∠γ 之间的关系为()A.∠α +∠β +∠γ =360°B.∠α -∠β +∠γ =180°C.∠α +∠β -∠γ =180°D.∠α +∠β +∠γ =180°3.如图,由A 到 B 的方向是()A.南偏东30°B.南偏东60°C.北偏西30°D.北偏西 60°4.如图,已知∠1=∠2,∠ BAD= ∠BCD ,则下列结论(1)AB//CD ;(2)AD//BC ;(3) ∠B=∠D;(4)∠D= ∠ACB 。其中正确的有()A 、1 个B、2 个C、3 个D、4 个、二、 填写理由1、已知:如图、BE//CF ,BE、 CF 分别平分∠ ABC 和∠ BCD 求证: AB//CD 证明: BE、平分∠ ABC (已知)∴∠ 1=21 ∠ CF 平分∠ BCD ()∠2=21 ∠() BE//CF (已知)∴∠ 1=∠2()∴21 ∠ ABC=21 ∠BCD ()即∠ ABC= ∠BCD ∴AB//CD ()2、如图,已知:∠BCF= ∠B+ ∠F。求证: AB//EF 证明:经过点C 作 CD//AB ∴∠ BCD= ∠B。() ∠ BCF= ∠B+∠ F,(已知)∴∠()=∠F。()A30oBNNABCDEA B C D 1 2 A C D F B E 1 2 B A E F C D ∴CD//EF 。()∴AB//EF ()3、已知,如图,BCE、AFE是直线, AB∥CD,∠ 1=∠2,∠ 3=∠4。求证: AD∥BE。证明: AB∥CD(已知)∴∠ 4=∠() ∠ 3=∠4(已知)∴∠ 3=∠() ∠ 1=∠2(已知)∴∠ 1+∠CAF=∠2+∠CAF()即∠ =∠∴∠ 3=∠()∴AD∥BE()四、解答题 (5 ×8) 1、若一个角的补角是它的余角的3 倍,求这个角的度数2、已知:如图,AB//CD ,BC//DE ,∠ B=70 ° ,求∠ D 的度数。3、已知: BC//EF ,∠ B=∠E,求证: AB//DE 。A D B C E F 1 2 3 4 A B E D C A B E P D C F 五、拓展提高。1.如图, AD⊥BC 于点 D,EF⊥BC 于点 F, EF 交 AB 于点 G,交 CA 的延长线于点E,且∠ 1=∠2.AD 平分∠ BAC 吗?说说你的理由.2. 如图,若 AB∥CD ,∠ 1=∠2,则∠ E=∠F,为什么?3、如图,将纸片△ABC 沿 DE 折叠,点 A 落在点 A′ 处,已知∠ 1+∠2=100 °,求 ∠A 的度数.1 2 A B C D E F A D B C 1 2 AE 1 2 A B C D F G E 4、如图,直线 AC∥BD,连结 AB...