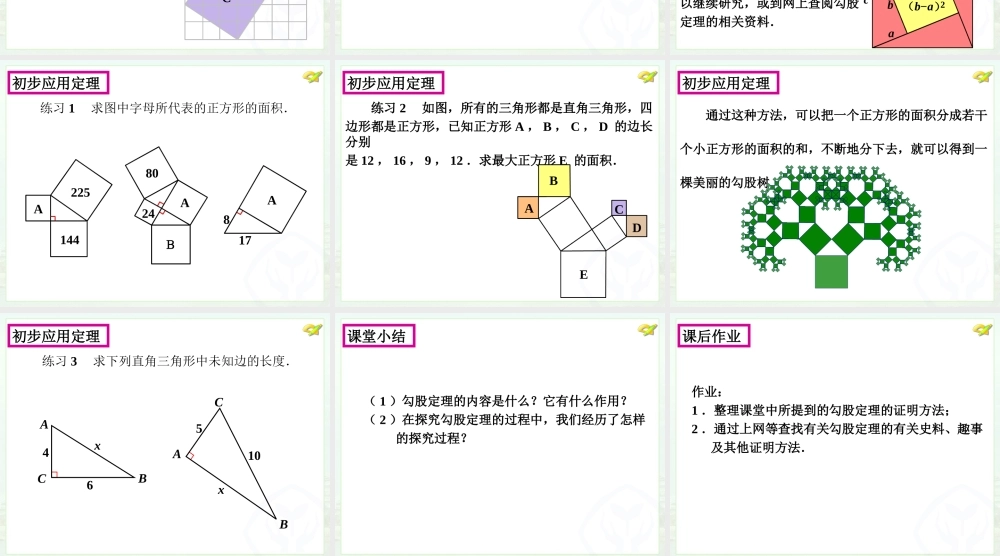
八年级 下册17.1 勾股定理( 1 )• 学习目标: 1 .经历勾股定理的探究过程,了解关于勾股定理 的一些文化历史背景,通过对于我国古代研究 勾股定理的成就的介绍,培养学生的民族自豪 感; 2 .能用勾股定理解决一些简单问题 .• 学习重点: 探索并证明勾股定理. 国际数学家大会是最高水平的全球性数学科学学术会议. 2002 年在北京召开了第 24 届国际数学家大会.如图就是大会的会徽的图案.创设情境 引入课题 问题 1 你见过这个图案吗?它由哪些基本图形组成? 追问 由这三个正方形A , B , C 的边长构成的等腰直角三角形三条边长度之间有怎样的特殊关系?创设情境 引入课题 问题 2 三个正方形 A , B , C 的面积有什么关系? A B C 追问 正方形 A 、 B 、 C 所围成的直角三角形三条边之间有怎样的特殊关系?探究勾股定理 问题 3 在网格中的一般的直角三角形,以它的三边为边长的三个正方形 A 、 B 、 C 是否也有类似的面积关系?A B C 猜想: 如果直角三角形两直角边长分别为 a , b ,斜边长为 c ,那么 a2+b2=c2 .探究勾股定理 问题 4 通过前面的探究活动,猜一猜,直角三角 形三边之间应该有什么关系? 感受数学文化 这个图案是公元 3 世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).勾股定理在数学发展中起到了重大的作用,其证明方法据说有 400 多种,有兴趣的同学可以继续研究,或到网上查阅勾股定理的相关资料.c b a (b-a)2 黄实 朱实 初步应用定理练习 1 求图中字母所代表的正方形的面积. A A A B 225 144 80 24 17 8 初步应用定理 练习 2 如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形 A , B , C , D 的边长分别是 12 , 16 , 9 , 12 .求最大正方形 E 的面积. A B C D E 初步应用定理 通过这种方法,可以把一个正方形的面积分成若干 个小正方形的面积的和,不断地分下去,就可以得到一 棵美丽的勾股树.初步应用定理练习 3 求下列直角三角形中未知边的长度. A B C 4 6 x C B A 5 10 x 课堂小结 ( 1 )勾股定理的内容是什么?它有什么作用?( 2 )在探究勾股定理的过程中,我们经历了怎样 的探究过程?课后作业 作业: 1 .整理课堂中所提到的勾股定理的证明方法;2 .通过上网等查找有关勾股定理的有关史料、趣事 及其他证明方法.