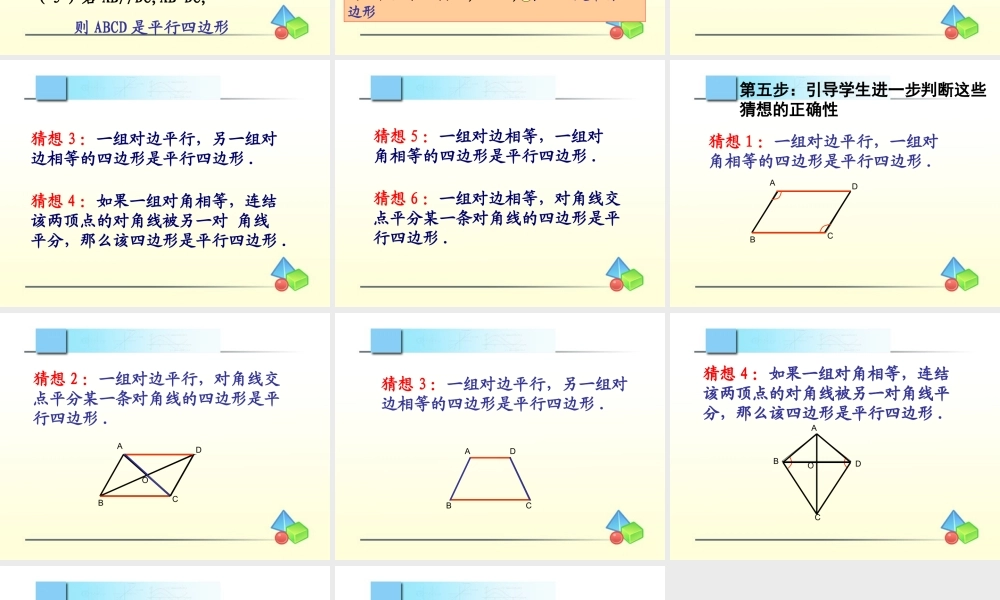
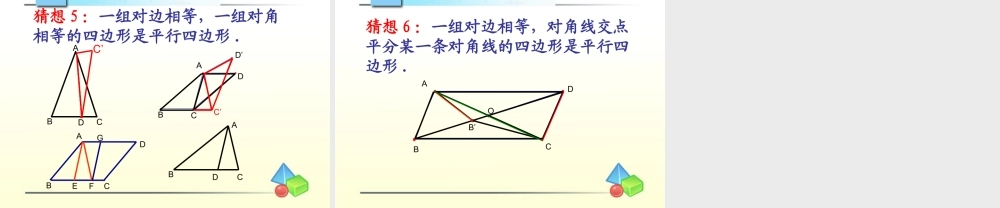
第一步:先带领学生回顾平行四边形的定义以及四条判定定理1. 平行四边形定义: 两组对边分别平行的四边形是平行四边形 2. 平行四边形判定定理:( 1 )两组对边分别相等的四边形 是平行四边形 .( 2 )对角线互相平分的四边形 是平行四边形 . ( 3 )两组对角分别相等的四边形 是平行四边形 .( 4 )一组对边平行且相等的四边形 是平行四边形 .2. 平行四边形判定定理: 第二步:把这些判定方法用数学语言表达出来 ( 1 )若 AB//DC,AD//BC, 则 ABCD 是平行四边形 . ( 2 )若 AB=DC,AD=BC, 则 ABCD 是平行四边形 .在四边形 ABCD 中, AC 与 BD 相交于 O. ( 3 )若 AO=OC,BO=OD, 则 ABCD 是平行四边形( 4 )若∠ A= ∠C,∠B=∠D, 则 ABCD 是平行四边形 ( 5 )若 AB//DC,AB=DC, 则 ABCD 是平行四边形在四边形 ABCD 中, AC 与 BD 相交于 O. 第三步:分析比较、创设问题情境( 1 )若 AB//DC,AD//BC, 则 ABCD 是平行四边形( 2 )若 AB=DC,AD=BC, 则 ABCD 是平行四边形( 3 )若 AO=OC,BO=OD, 则 ABCD 是平行四边形( 4 )若∠ A= ∠C,∠B=∠D, 则 ABCD 是平行四边形( 5 )如果 AB//DC,AB=DC, 则 ABCD 是平行四边形平行相等平行、相等 第四步:学生提出猜想猜想 1 :一组对边平行,一组对角相等的四边形是平行四边形 .猜想 2 :一组对边平行,对角线交点平分某一条对角线的四边形是平行四边形 . 猜想 3 :一组对边平行,另一组对边相等的四边形是平行四边形 .猜想 4 :如果一组对角相等,连结该两顶点的对角线被另一对 角线平分,那么该四边形是平行四边形 . 猜想 5 :一组对边相等,一组对角相等的四边形是平行四边形 .猜想 6 :一组对边相等,对角线交点平分某一条对角线的四边形是平行四边形 . ABCD猜想 1 :一组对边平行,一组对角相等的四边形是平行四边形 .第五步:引导学生进一步判断这些猜想的正确性 ABCDO猜想 2 :一组对边平行,对角线交点平分某一条对角线的四边形是平行四边形 . 猜想 3 :一组对边平行,另一组对边相等的四边形是平行四边形 .ABCD 猜想 4 :如果一组对角相等,连结该两顶点的对角线被另一对角线平分,那么该四边形是平行四边形 .猜想 4 :如果一组对角相等,连结该两顶点的对角线被另一对角线平分,那么该四边形是平行四边形 .ABCDO 猜想 5 :一组对边相等,一组对角相等的四边形是平行四边形 .DCBAC’ABCDC’D’ABCDEFGABCD ABCDOB’猜想 6 :一组对边相等,对角线交点平分某一条对角线的四边形是平行四边形 .