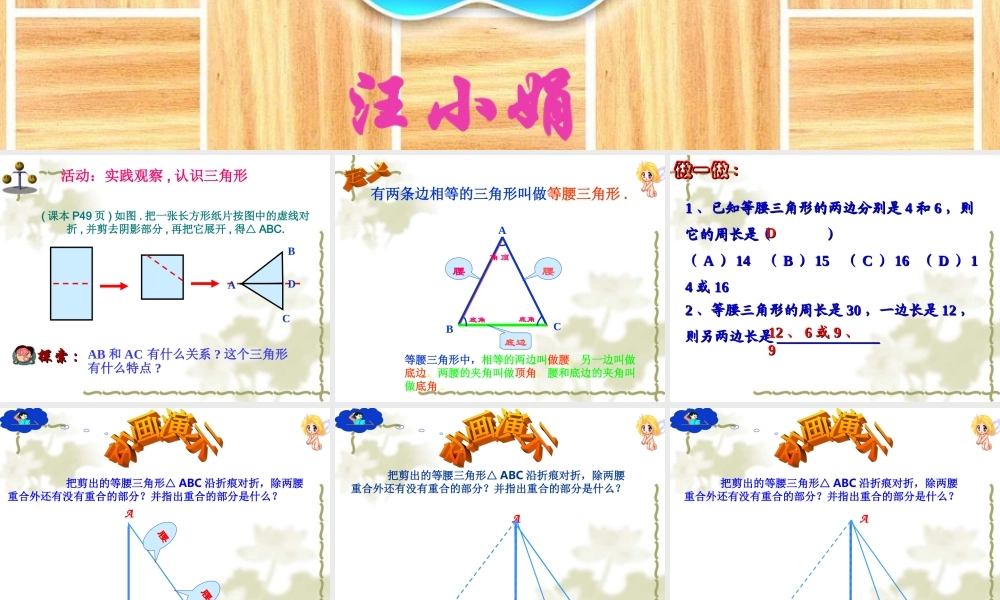
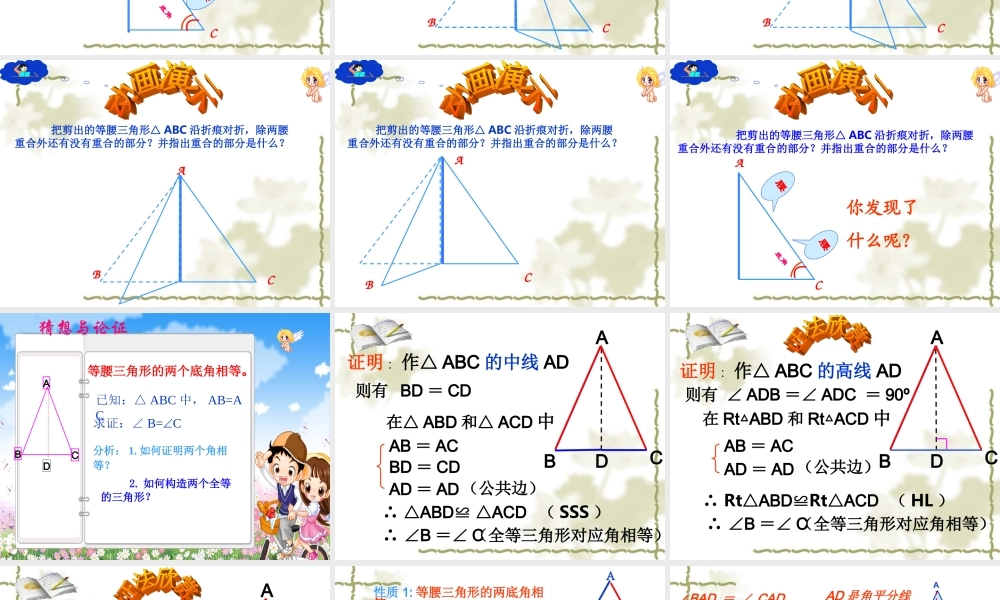
12.3.1等腰三角形的性质汪小娟 ( 课本 P49 页 ) 如图 . 把一张长方形纸片按图中的虚线对折 , 并剪去阴影部分 , 再把它展开 , 得△ ABC. 活动:实践观察 , 认识三角形AB 和 AC 有什么关系 ? 这个三角形有什么特点 ?探索探索 :: CADB 有两条边相等的三角形叫做等腰三角形 . 等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角 .ACB腰腰底边顶角底角底角 11 、已知等腰三角形的两边分别是、已知等腰三角形的两边分别是 44 和和 66 ,则,则它的周长是( )它的周长是( )(( AA )) 14 14 (( BB )) 15 15 (( CC )) 16 16 (( DD )) 1144 或或 1616DD22 、等腰三角形的周长是、等腰三角形的周长是 3030 ,一边长是,一边长是 1212 ,,则另两边长是则另两边长是 ____________________________1212 、、 66 或或 99 、、99做一做做一做 :: AC 把剪出的等腰三角形△ ABC 沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? 腰腰底角 ABC 把剪出的等腰三角形△ ABC 沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? ABC 把剪出的等腰三角形△ ABC 沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? ABC 把剪出的等腰三角形△ ABC 沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? ABC 把剪出的等腰三角形△ ABC 沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? AC 把剪出的等腰三角形△ ABC 沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? 腰腰底角你发现了什么呢? 猜想与论证等腰三角形的两个底角相等。已知:△ ABC 中, AB=AC求证:∠ B=C分析: 1. 如何证明两个角相等? 2. 如何构造两个全等的三角形?ABCD ABC则有 BD = CDD在△ ABD 和△ ACD 中证明 : 作△ ABC 的中线 ADAB = AC BD = CDAD = AD (公共边) ∴ △ABD≌ △ACD ( SSS ) ∴ ∠B =∠ C (全等三角形对应角相等) ABC则有 ∠ ADB =∠ ADC = 90ºD在 Rt ABD△和 Rt ACD△中证明 : 作△ ABC 的高线 ADAB = AC AD = AD (公共边) ∴ Rt△ABD≌Rt△ACD ( HL ) ∴ ∠B =∠ C (全等三角形对...