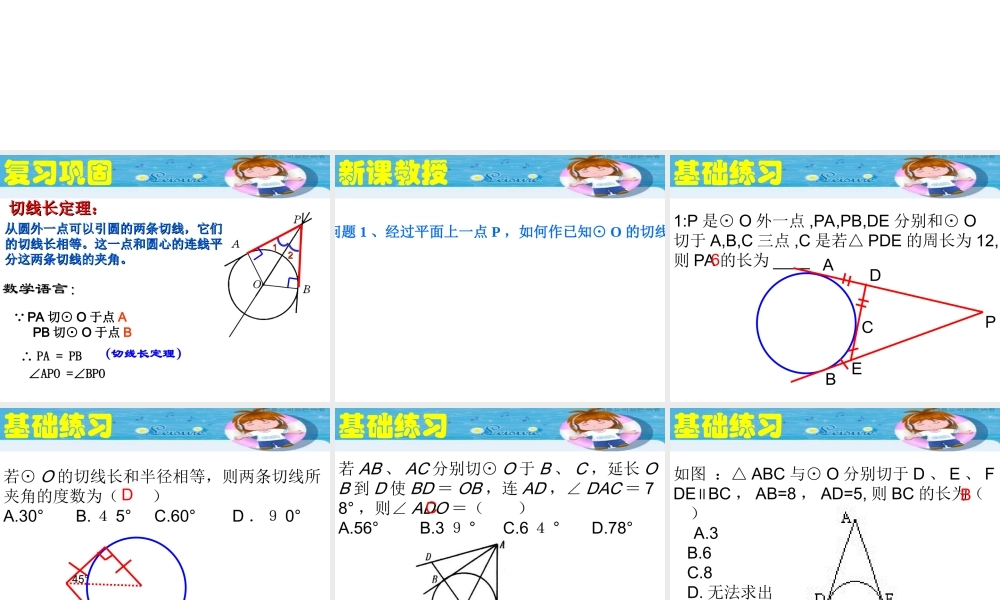
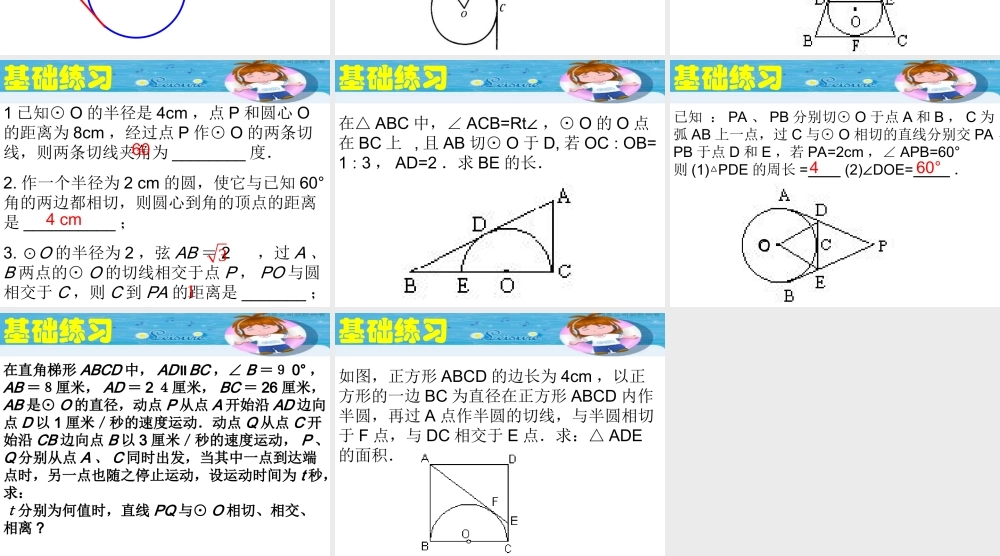
切线长定理练习课 复习巩固∴ PA == PB∠APO ==∠BPO切线长定理:切线长定理:数学语言:数学语言: ∵ PA 切⊙ O 于点 A PB 切⊙ O 于点 B(切线长定理)从圆外一点可以引圆的两条切线,它们从圆外一点可以引圆的两条切线,它们的切线长相等。这一点和圆心的连线平的切线长相等。这一点和圆心的连线平分这两条切线的夹角。 分这两条切线的夹角。 1122 新课教授问题 1 、经过平面上一点 P ,如何作已知⊙ O 的切线? 基础练习1:P 是⊙ O 外一点 ,PA,PB,DE 分别和⊙ O切于 A,B,C 三点 ,C 是若△ PDE 的周长为 12,则 PA 的长为 ____ APBDEC6 基础练习若⊙ O 的切线长和半径相等,则两条切线所夹角的度数为( )A.30° B. 4 5° C.60° D .9 0°45°D 基础练习若 AB 、 AC 分别切⊙ O 于 B 、 C ,延长 OB 到 D 使 BD = OB ,连 AD ,∠ DAC = 78° ,则∠ ADO =( )A.56° B.3 9 ° C.6 4 ° D.78°C 基础练习如图 :△ ABC 与⊙ O 分别切于 D 、 E 、 F ,DE BC∥, AB=8 , AD=5, 则 BC 的长为( ) A.3 B.6 C.8 D. 无法求出B 基础练习1 已知⊙ O 的半径是 4cm ,点 P 和圆心 O的距离为 8cm ,经过点 P 作⊙ O 的两条切线,则两条切线夹角为 ________ 度. 602. 作一个半径为 2 cm 的圆,使它与已知 60°角的两边都相切,则圆心到角的顶点的距离是 __________ ; 4 cm3. ⊙O 的半径为 2 ,弦 AB = 2 ,过 A 、B 两点的⊙ O 的切线相交于点 P , PO 与圆相交于 C ,则 C 到 PA 的距离是 _______ ;13 基础练习在△ ABC 中,∠ ACB=Rt∠ ,⊙ O 的 O 点在 BC 上 , 且 AB 切⊙ O 于 D, 若 OCOB=∶13∶ , AD=2 .求 BE 的长. 基础练习已知 : PA 、 PB 分别切⊙ O 于点 A 和 B , C 为弧 AB 上一点,过 C 与⊙ O 相切的直线分别交 PA 、PB 于点 D 和 E ,若 PA=2cm ,∠ APB=60°则 (1) PDE△的周长 = (2) DOE=∠ .4O60° 基础练习在直角梯形 ABCD 中, AD∥BC ,∠ B =9 0° ,AB =8厘米, AD = 2 4厘米, BC = 26 厘米,AB 是⊙ O 的直径,动点 P 从点 A 开始沿 AD 边向点 D 以 1 厘米/秒的速度运动.动点 Q 从点 C 开始沿 CB 边向点 B 以 3 厘米/秒的速度运动, P 、Q 分别从点 A 、 C 同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为 t 秒,求:t分别为何值时,直线 PQ 与⊙ O 相切、相交、相离 ? 基础练习如图,正方形 ABCD 的边长为 4cm ,以正方形的一边 BC 为直径在正方形 ABCD 内作半圆,再过 A 点作半圆的切线,与半圆相切于 F 点,与 DC 相交于 E 点.求:△ ADE的面积.