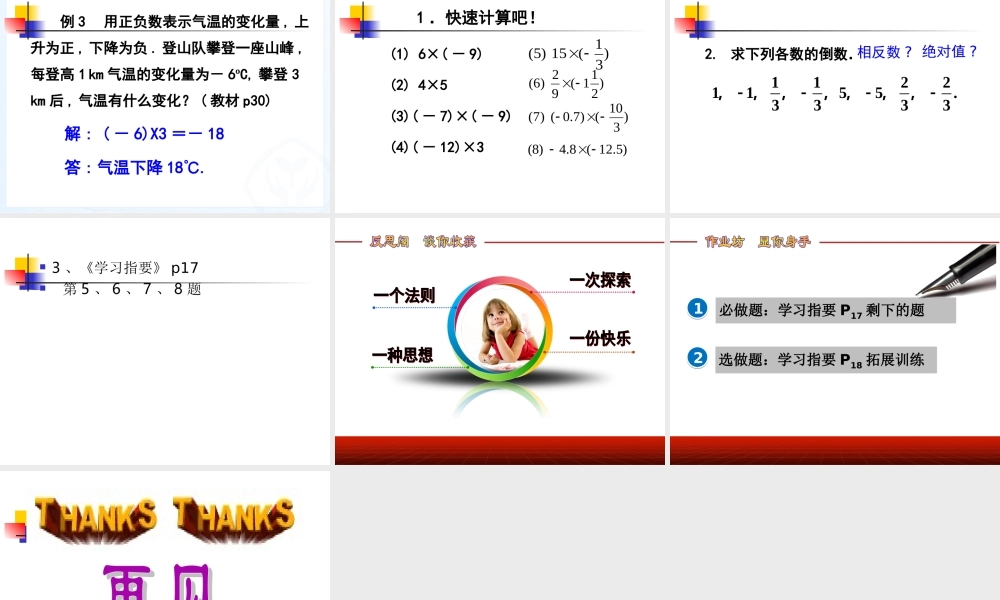
(1)( - 4) + ( -6)(2) 18 + ( - 6)(3)( - 13) + 6(4)( - 4.3) +4.3(5)( - 0.9) +1.5(6) 0 + ( - 6)(7) 12()23+ -= -( )4+6= -10= -( )18-6 = -12= -( )13-6 = -7= 0= +( )1.5-0.9= 0.6= -6)2132(611 .同号两数相加,取相同的符号,并把绝对值相加;2 .异号两数相加时: (1) 若绝对值不相等,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值; (2) 若绝对值相等,和为 0. 即互为相反数的两个数和为 0 ;3 .一个数与 0 的和仍得这个数 . 有理数加法法则1.4 1.4 有理数的乘除法(第有理数的乘除法(第 11 课时)课时)1.4.1 1.4.1 有理数的乘法(有理数的乘法( 11 ))义务教育教科书 数学 七年级 上册观察下面的乘法算式 , 你能发现什么规律吗 ? 随着后一乘数 逐次递减 1,积逐次递减 3 . 3×3 = 9 3×2 = 6 3×1 = 3 3×0 = 0 3×(-1) 3×(-2) 3×(-3)=- 3 =- 6 =- 9正数乘正数 ,积为正数.正数乘 0, 积为 0 .正数乘负数 ,积为负数.类比上述研究过程 , 你又能发现什么规律呢 ?随着前一乘数 逐次递减 1,积逐次递减 3 . 3×3 = 9 2×3 = 6 1×3 = 3 0×3 = 0 (-1)×3 (-2)×3 (-3)×3=- 3 =- 6 =- 9负数乘正数 ,积为负数.正数乘 0, 积为 0 .从符号和绝对值两个角度观察 , 可归纳积的特点:正数乘正数,积为正数;正数乘负数,积为负数;负数乘正数,积为负数; 积的绝对值等于各乘数绝对值的积.利用上面归纳的结论计算下面的算式 , 你发现什么规律 ?随着后一乘数 逐次递减 1,积逐次递增 3 . (-3)×3 = (-3)×2 = (-3)×1 = (-3)×0 = (-3)×(-1) (-3)×(-2) (-3)×(-3)= 3 = 6 = 9负数乘负数 ,积为正数.- 9 - 6 - 3 0有理数乘法法则: 两数相乘,同号得正,异号得负, 并把绝对值相乘.任何数与 0 相乘,都得 0.请理解记忆,请说给同桌听 .若 a>0,b>0, 则 ab>0;若 a<0,b<0, 则 ab>0;若 a>0,b<0, 则 ab<0;若 a<0,b>0, 则 ab<0;a×0 = 0( 5) ( 3) ………… 同号两数相乘 得正= 15 .( 7) 4( 2 )( 1 )= + ( )………,并把绝对值相乘5×3………… 异号两数相乘 得负= -( ) ………,并把绝对值相乘7×4= -28思考:通过上题,你认...