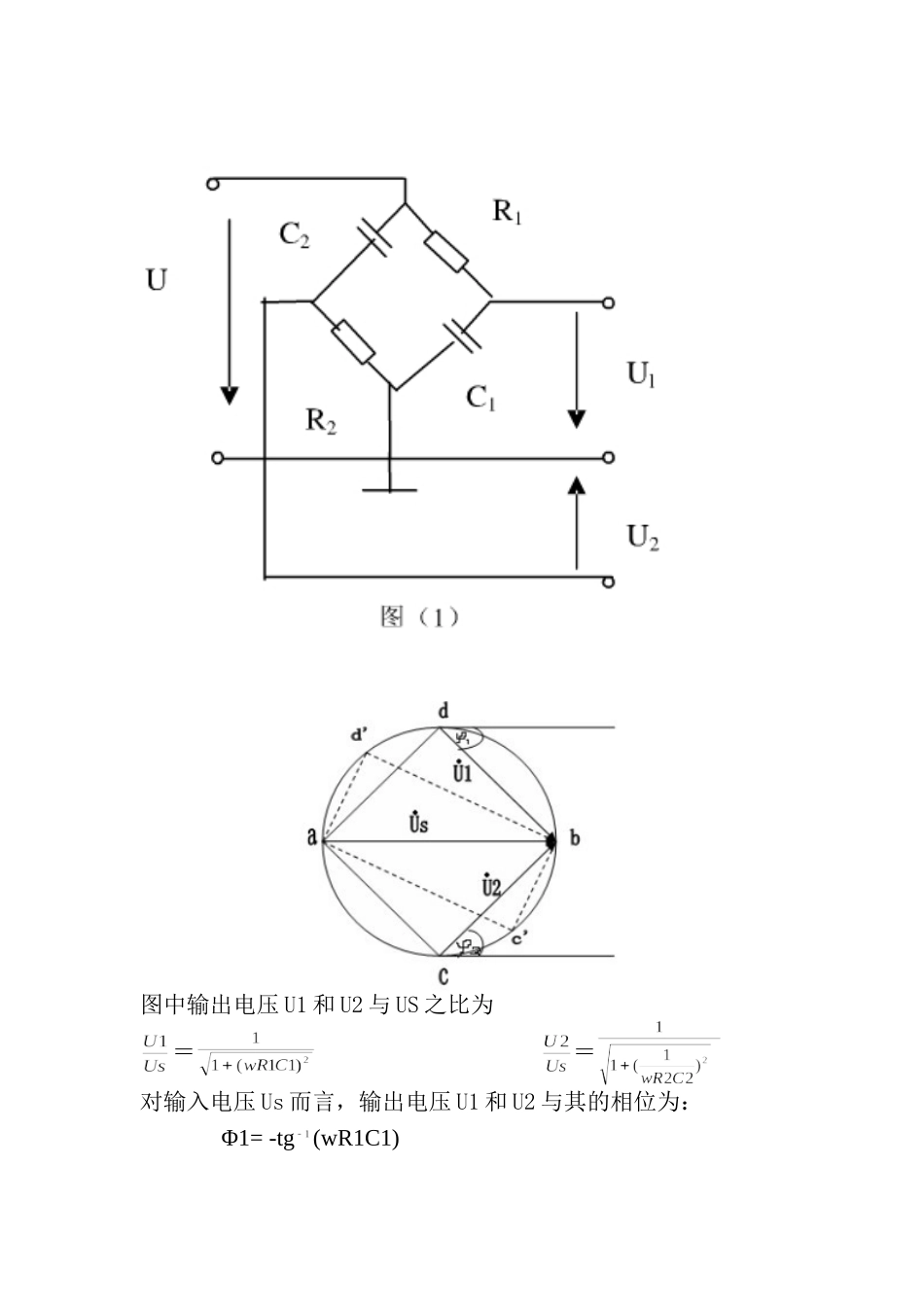
电子电工综合实验论文裂相电路姓名:杨颖班级:10042401学号:1004240108裂相(分相)电路摘要:裂相电路仅由电容和电阻构成,利用电容的阻抗与电阻分压,同时利用电容对电压相位的移位性质,从而能把一个单相交流电压设计出两个电压幅值相等,相位相差90度的两相交流电压。分析了优化RC桥式裂相电路的方法,选取了优化方案研究了RC桥式裂相电路中电压与负载的关系(裂相电路电压与电阻性阻抗、电容性阻抗、电感性阻抗的关系),裂相电路负载的功耗与所接负载的关系。关键词:裂相两相电源电压-负载特性引言:利用裂相电路实现对交流电源的分相,满足了对多电源的需求,具有较好的现实意义。设计要求:一、将单相交流电源(220V/50Hz)分裂成相位差为90°的两相电源。1.两相输出空载时电压有效值相等,为155×(1±2%)V;相位差为90°×(1±2%)2.测量并作电压—负载(两负载相等,且为电阻性)特性曲线,到输出电压150×(1-10%);相位差为90°×(1-5%)为止。3.测量证明设计的电路在空载时功耗最小。二、若负载分别为感性或容性时,讨论电压—负载特性。三、论述分相电路的用途,并举一例详细说明。实验原理:将单相变为两相把电源Us分裂成U1和U2输出电压,如下图所示为RC桥式分相电压原理,可以把输入电压分成两个有效值相等,相位相差90度的两个电压源。图中输出电压U1和U2与US之比为==对输入电压Us而言,输出电压U1和U2与其的相位为:Φ1=-tg(wR1C1)Φ2=tg()或ctgφ2=wR2C2=-tg(φ2+90°)由此φ2+90°=-tg(wR2C2)若R1C1=R2C2=RC则必有φ1-φ2=90°一般而言,φ1和φ2与角频率w无关,但为使U1与U2数值相等可令wR1C1=wR2C2=1下面是具体的实验电路图以及数据:1.两相输出空载时电压有效值相等,为155×(1±2%)V;相位差为90°×(1±2%)。上面的万用表显示空载电压有效值为155V左右,仿真图显示相位相差为90度左右。其中,实验的电压源为220V,50HZ。取R1=R2=R=300C1=C2=C=10.6F,所设定的数据满足wR1C1=wR2C2=1,且经过取多组值比较可得取该组值时所得实验数据较好。2.测量并作电压负载(两负载相等,且为电阻性)特性曲线,到输出电压150(1-10%)V;相位差为90°×(1-5%)为止。令负载R3=R4=,并变换阻值时测量负载两端的电压。下面为实验数据:(备注:由于R1=R2=,并且在测量中发现两负载的电压和功耗都近似相等,故只绘制U1-和P1-曲线。)下面是根据实验数据绘制的V-和P-曲线0123456x105120125130135140145150155160Ω电阻()(V)电压00.511.522.533.544.55x10502468101214Ω电阻()W功率()在输出电压-负载图中,虚线表示电源衰减了10﹪时,所对应的负载为1500Ω左右。在衰减10﹪范围内随着负载阻值的减少,负载两端的电压逐渐降低,功耗逐渐增大。下面从理论上来证明上述结论。如图:R1R2r3r4C1C2U设负载电阻为R1=R2=,裂相电阻为r3=R4=R,电容为C1=C2=C,为负载R1的电压,为负载R2上的电压。因为=r所以:对于左边的负载有:===相位满足对于右边的负载有:====相位满足所以当负载变化时两相电源的相位差恒定为。由此可见是负载R的增函数,并且。这与实验所测数据相吻合。当电压衰减了10﹪时,=R=4.715r=1414.6Ω,这与实验仿真得到的临界电阻一致。现在把具体的数据代入:U=220Vr=300ΩC=10.6F,则有:==(V)用matlab绘制出理论曲线:0.511.522.533.544.555.56x104020406080100120140160R(Ω)U(V)与实验仿真所绘制出的U-R图比较可知,两条曲线是一致的。下面从理论上来推导两负载的功率:由于==故有:==由表达式可知当负载很小时,功率P随着的增大而增大,有一个最大值为=,此时有负载=。然功率随着的进一步增大而减少,当负载为无穷,即空载时功率最小,为零。并且我们推出=,这与先前仿真出的结果完全一致。现在我们把仿真数据U=220Vr=300ΩC=10.6F代入式中:==(W)功率峰值出现在==212.132Ω=33.413W下面是用matlab所绘制出的P-曲线:由于功率取极大值时电阻很小为212.132Ω,所以本图中的电阻间隔相比于仿真的出的曲线图中的要小的多。而实验仿真到电压源衰减了10﹪时就停止仿真,此时负载电阻为1500Ω左右,故看不到P-曲线的极大值部分,而只看到了功率随着电阻的...