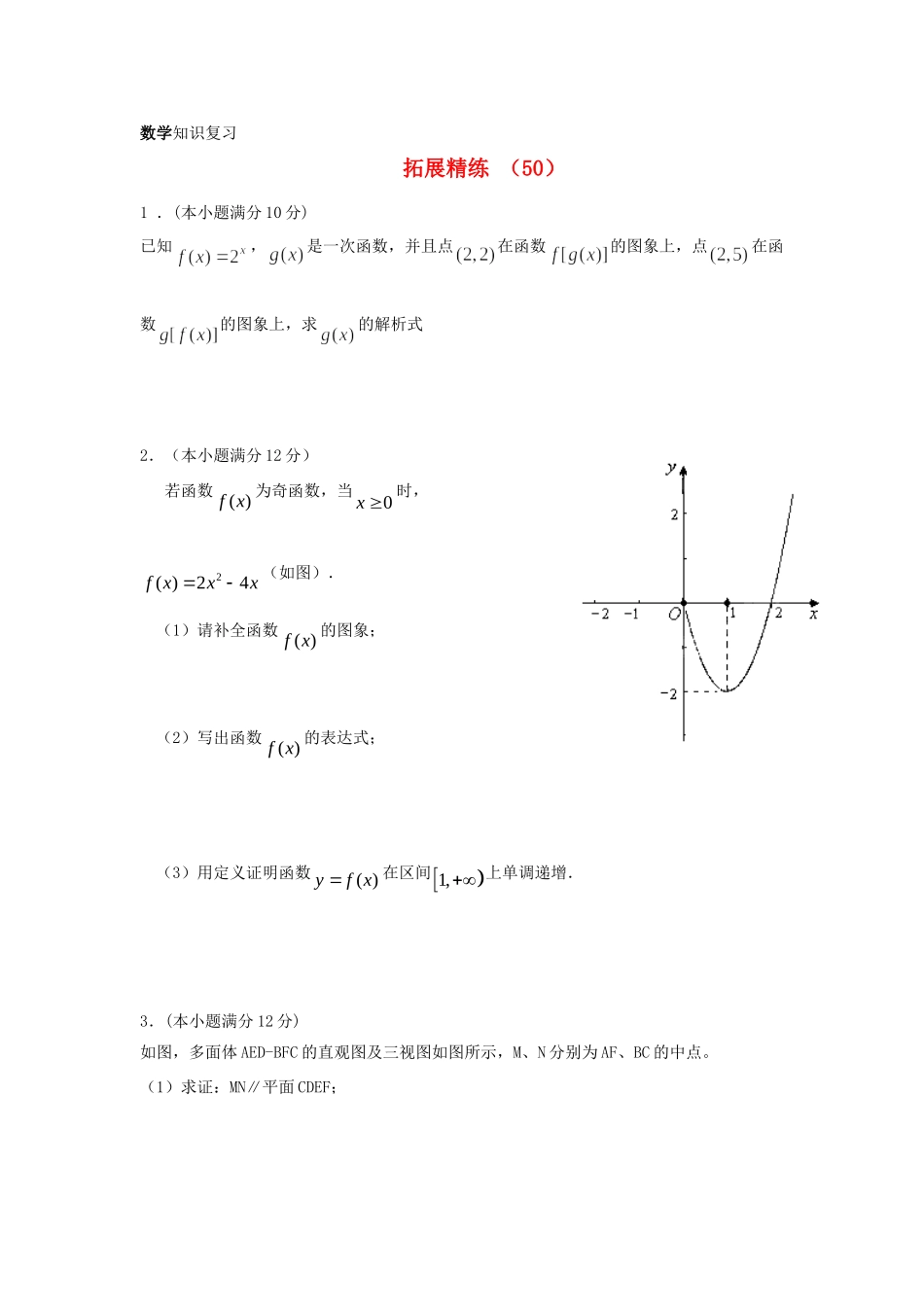
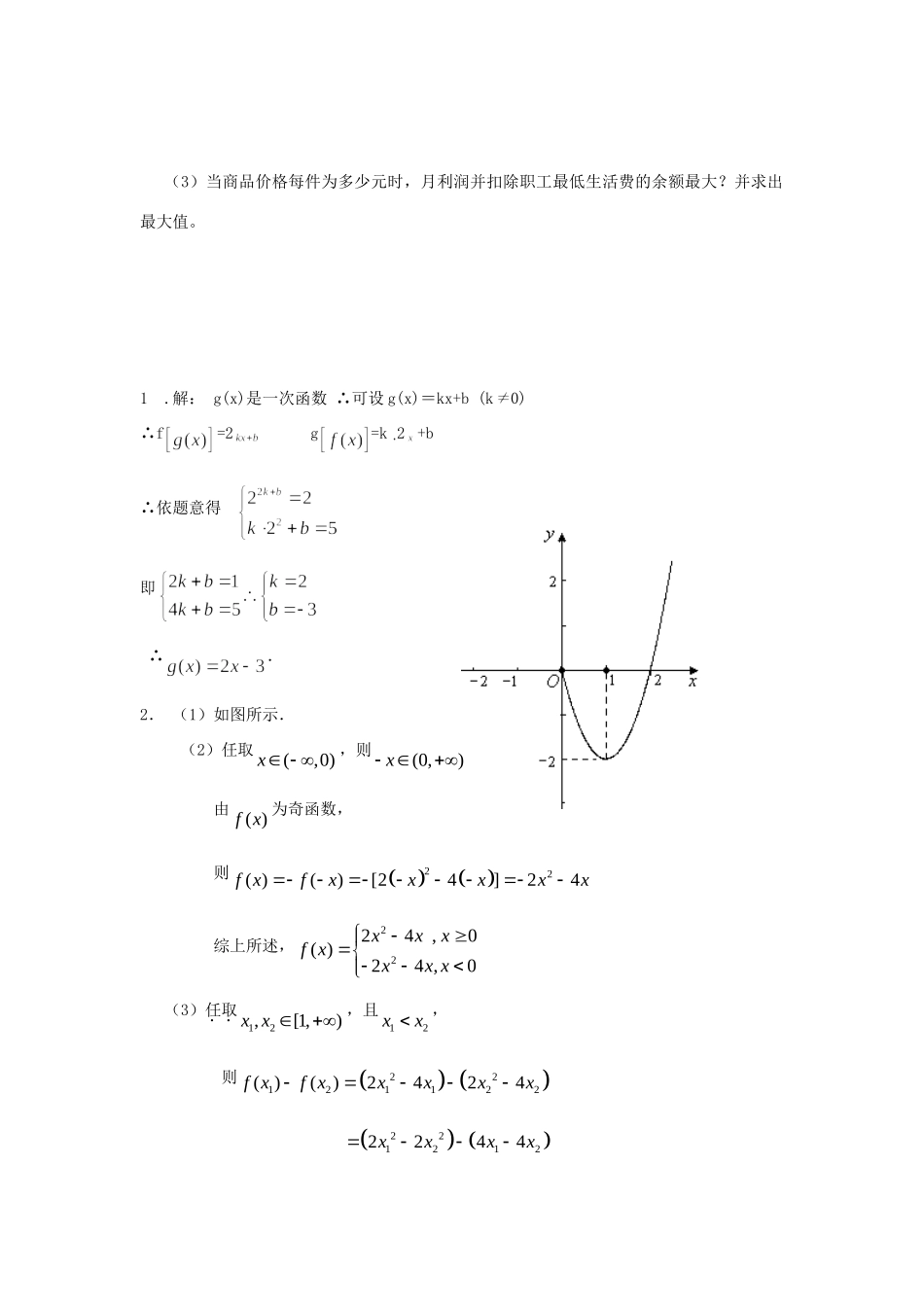
数学知识复习 拓展精练 (50)1 .(本小题满分 10 分)已知,是一次函数,并且点在函数的图象上,点在函数的图象上,求的解析式2.(本小题满分 12 分)若函数( )f x 为奇函数,当0x 时,2( )24f xxx(如图).(1)请补全函数( )f x 的图象;(2)写出函数( )f x 的表达式;(3)用定义证明函数( )yf x在区间1, 上单调递增. 3.(本小题满分 12 分)如图,多面体 AED-BFC 的直观图及三视图如图所示,M、N 分别为 AF、BC 的中点。(1)求证:MN∥平面 CDEF;(2)求多面体 A-CDEF 的体积; (3)求证:。4.(本小题满分 12 分)已知函数 f(x)=lg(ax-bx)(a>1>b>0).(1)求 y=f(x)的定义域;(2)在函数 y=f(x)的图象上是否存在不同的两点,使得过这两点的直线平行于 x 轴;(3)当 a,b 满足什么条件时,f(x)在(1,+∞)上恒取正值.5.(本小题满分 12 分)直线 l 经过点,且和圆 C:相交,截得弦长为,求 l 的方程. 6(本小题满分 14 分)某商店经营的消费品进价每件 14 元,月销售量 Q(百件)与销售价格 P(元)的关系如下图,每月各种开支 2000 元,(1)写出月销售量 Q(百件)与销售价格 P(元)的函数关系。 (2)该店为了保证职工最低生活费开支 3600 元,问:商品价格应控制在什么范围? (3)当商品价格每件为多少元时,月利润并扣除职工最低生活费的余额最大?并求出最大值。1 .解: g(x)是一次函数 ∴可设 g(x)=kx+b (k0)∴f=2 g=k 2 +b ∴依题意得 即 ∴.2. (1)如图所示. (2)任取(,0)x ,则(0,)x由( )f x 为奇函数,则22( )()[24]24f xfxxxxx 综上所述,2224,0( )24 ,0xxxf xxx x (3)任取12,[1,)x x ,且12xx, 则12( )()f xf x 2211222424xxxx 2212122244xxxx12121224xxxxxx 12122[2]xxxx 12xx ∴120xx又由12,[1,)x x ,且12xx,所以122xx,∴1220xx∴ 12122[2]0xxxx,∴12( )()0f xf x,即12( )()f xf x ∴函数2( )24f xxx在区间1, 上单调递增。3.(1)证明:由多面体 AED-BFC 的三视图知,三棱柱 AED-BFC 中,底面 DAE 是等腰直角三角形,...