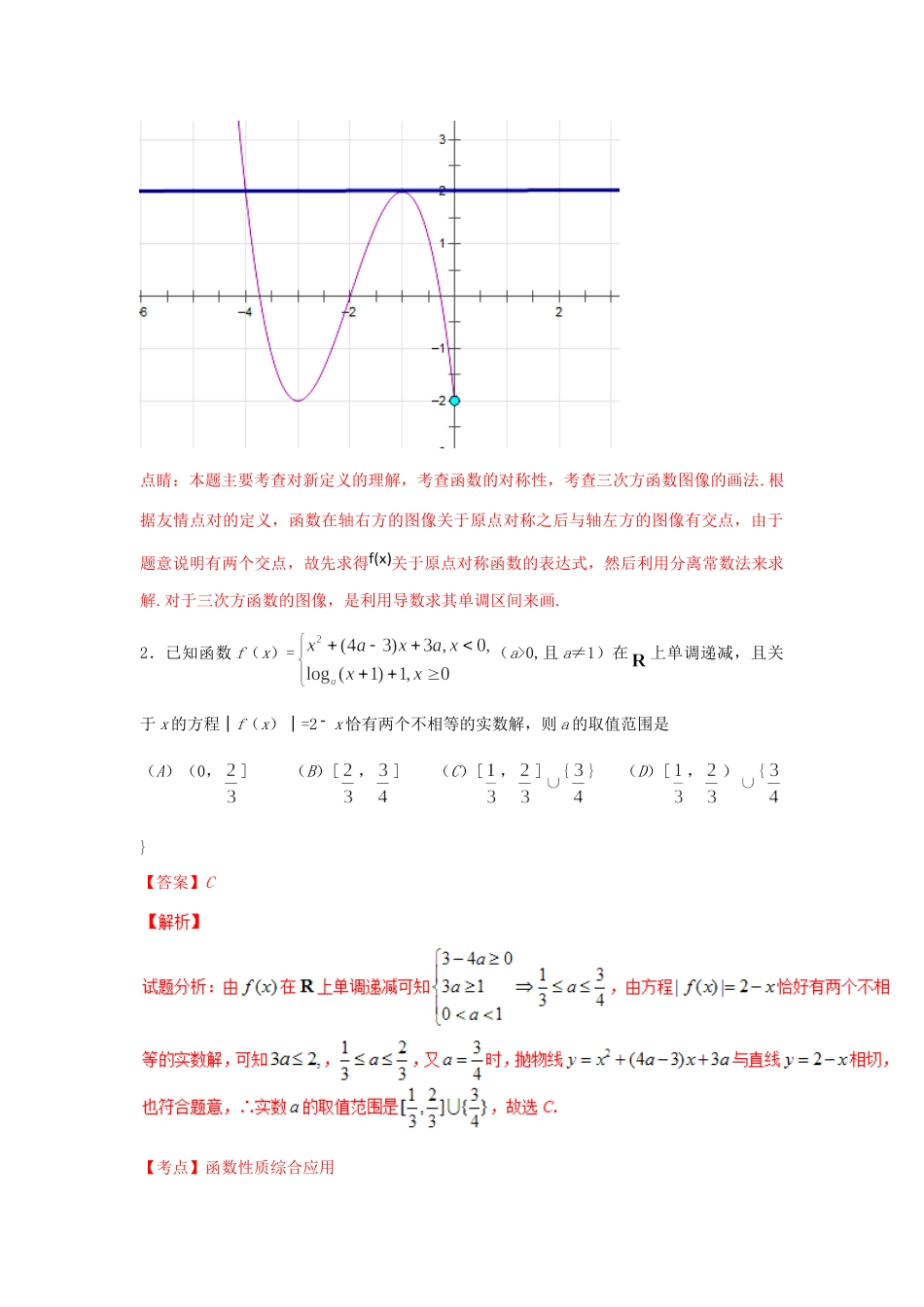
2017-2018 学年高一数学上学期期末复习备考之精准复习模拟题2(B 卷)新人教版考试时间:120 分钟;总分:150 分题号一二三总分得分注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第 I 卷(选择题)评卷人得分一、单选题(每小题 5 分,共计 60 分)1.若函数的图象上存在两个点关于原点对称,则称点对为的“友情点对”,点对与可看作同一个“友情点对”,若函数恰好由两个“友情点对”,则实数 的值为( )A. B. 2 C. 1 D. 0【答案】B【解析】首先注意到没有对称点.当时,,则,即有 两 个 实 数 根 , 即有 两 个 实 数 根 . 画 出的图像如下图所示,由图可知时有两个解.点睛:本题主要考查对新定义的理解,考查函数的对称性,考查三次方函数图像的画法.根据友情点对的定义,函数在轴右方的图像关于原点对称之后与轴左方的图像有交点,由于题意说明有两个交点,故先求得关于原点对称函数的表达式,然后利用分离常数法来求解.对于三次方函数的图像,是利用导数求其单调区间来画.2.已知函数 f(x)=(a>0,且 a≠1)在上单调递减,且关于 x 的方程│f(x)│=2x 恰有两个不相等的实数解,则 a 的取值范围是(A)(0,] (B)[,] (C)[,]{} (D)[,){}【答案】C【考点】函数性质综合应用【名师点睛】已知函数有零点求参数取值范围常用的方法和思路:(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.3.函数 的部分图象如图所示,则函数的一个表达式为A. B. C. D. 【答案】A【解析】由函数的图象可得最大值为 4,且在一周期内先出现最小值,所以,观察图象可得函数的周期 T=16, ,若,则当时, , ;当又函数的图象过(2,﹣4)代入可得,∴, ,∴函数的表达式.故选 A.4.下列函数中,既是偶函数又在上单调递增的函数是( )A. B. C. D. 【答案】C5.平面内已知向量,若向量与方向相反,且,则向量( )A. B. C. D. 【答案】B【解析】 向量与方向相反,∴, ,∴,则|x|=2,x=2− ,即=2(2,1)=(4,2)−−−,本题选择 B 选项.6.平面向量与的夹角为, , ,则( ).A. B. C. D. 【答案】C【解析】 与的夹角为, , ,...