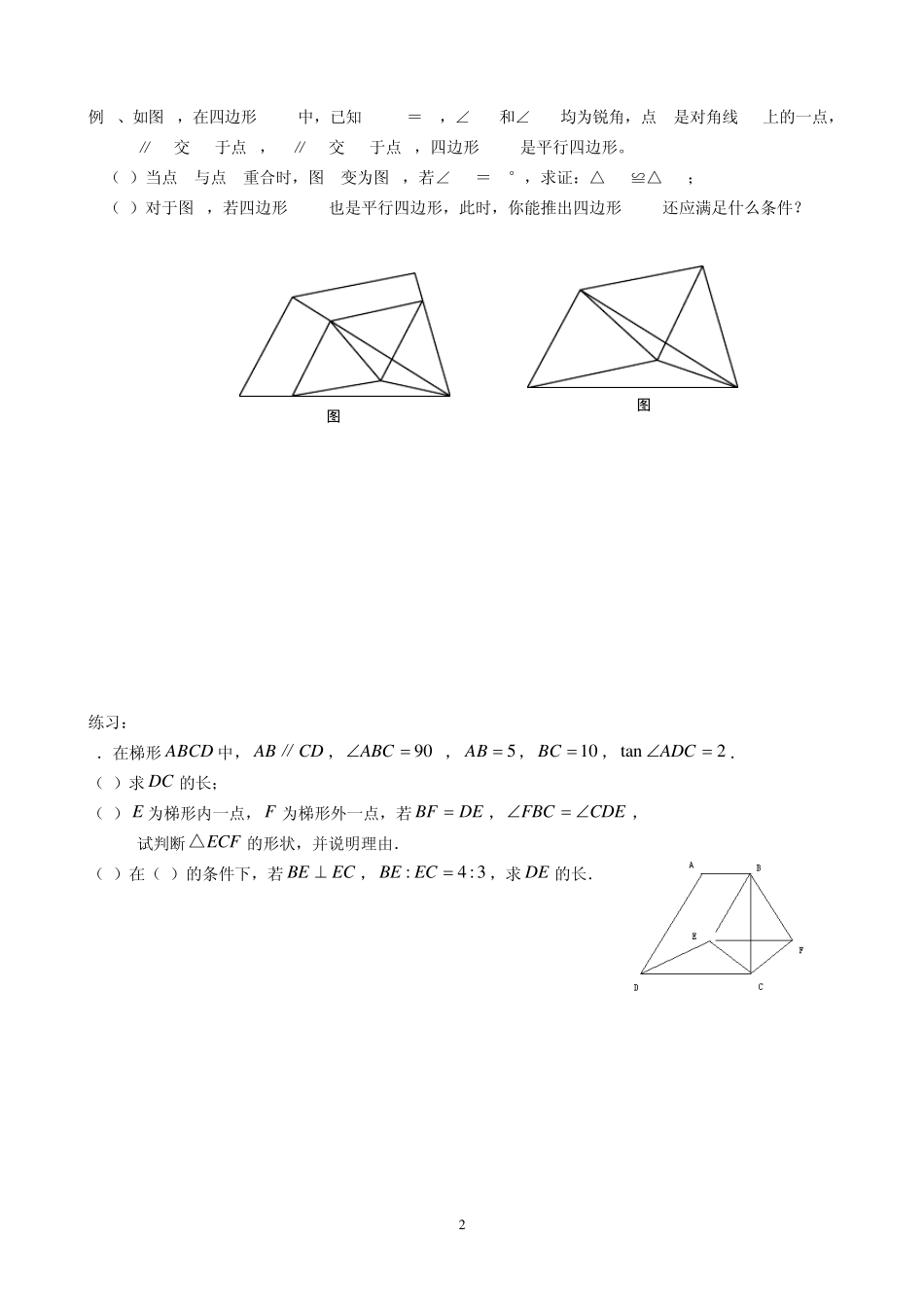
1 中考总复习---几何综合 几何综合题常研究以下几个方面的问题: 1.证明线段、角的数量关系(包括相等、和差、倍、分关系以及比例关系); 2.证明图形的位置关系(如点与线、线与线、线与圆等); 3.面积计算问题; 4.动态几何问题 在解几何综合问题时,常要分解基本图形,挖掘隐含的数量关系,另外,也需要注意使用数形结合、方程、分类讨论等数学思想方法来解决问题。借助变换的观点也能帮助我们找到更有效的解决问题的思路。 解几何综合题,要充分利用综合与分析的思维方法。当思维受阻时要及时改变方向;要熟悉常用的辅助线添法;强化变换的意识;从特殊或极端位置探究结论。 第一课时:基本证明与计算: 例 1.直线 CF垂直且平分 AD于点 E,四边形 ABCD是菱形,BA的延长 线交CF于点 F,连接AC。 (1)写出图中两对全等三角形。 (2)求证:ΔABC是正三角形。 例 2、在平行四边形 ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G. (1 ) 求证:ΔADE≌ΔCBF (2 ) 若四边形 BEDF是菱形,则四边形 AGBD是什么特殊四边形?并证明你的结论。 2 例3、如图1,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点P是对角线BD上的一点,PQ∥BA交AD于点Q,PS∥BC交DC于点S,四边形PQRS是平行四边形。 (1)当点P与点B重合时,图1变为图2,若∠ABD=90°,求证:△ABR≌△CRD; (2)对于图1,若四边形PRDS也是平行四边形,此时,你能推出四边形ABCD还应满足什么条件? 练习: 1.在梯形ABCD 中,ABCD∥,90ABC°,5AB ,10BC ,tan2ADC. (1)求 DC 的长; (2)E为梯形内一点,F 为梯形外一点,若BFDE,FBCCDE , 试判断ECF△的形状,并说明理由. (3)在(2)的条件下,若BEEC,:4 :3BE EC ,求 DE 的长. 图2图1RDCBASRPQDCBA 3 EABPCD2.如图,四边形ABCD为一梯形纸片,AB//CD,AD=BC.翻折纸片ABCD, 使点A与点C重合,折痕为EF.已知CE⊥AB. (1)求证:EF//BD; (2)若AB=7,CD=3,求线段EF的长. 3.已知:在ABC△中,D为AB边上一点,3 6A,ACBC,ADABAC2 (1)试说明:ADC△和BDC△都是等腰三角形; (2)若1AB ,求AC 的值; (3)请你构造一个等腰梯形,使得该梯形连同它的两条对角线得到8个等腰三角形.(标明各角的度数) 4.如图,AB⊥BC,DC⊥BC,垂足分别为B、C。 (1) 当AB=4,DC=1,BC=4...