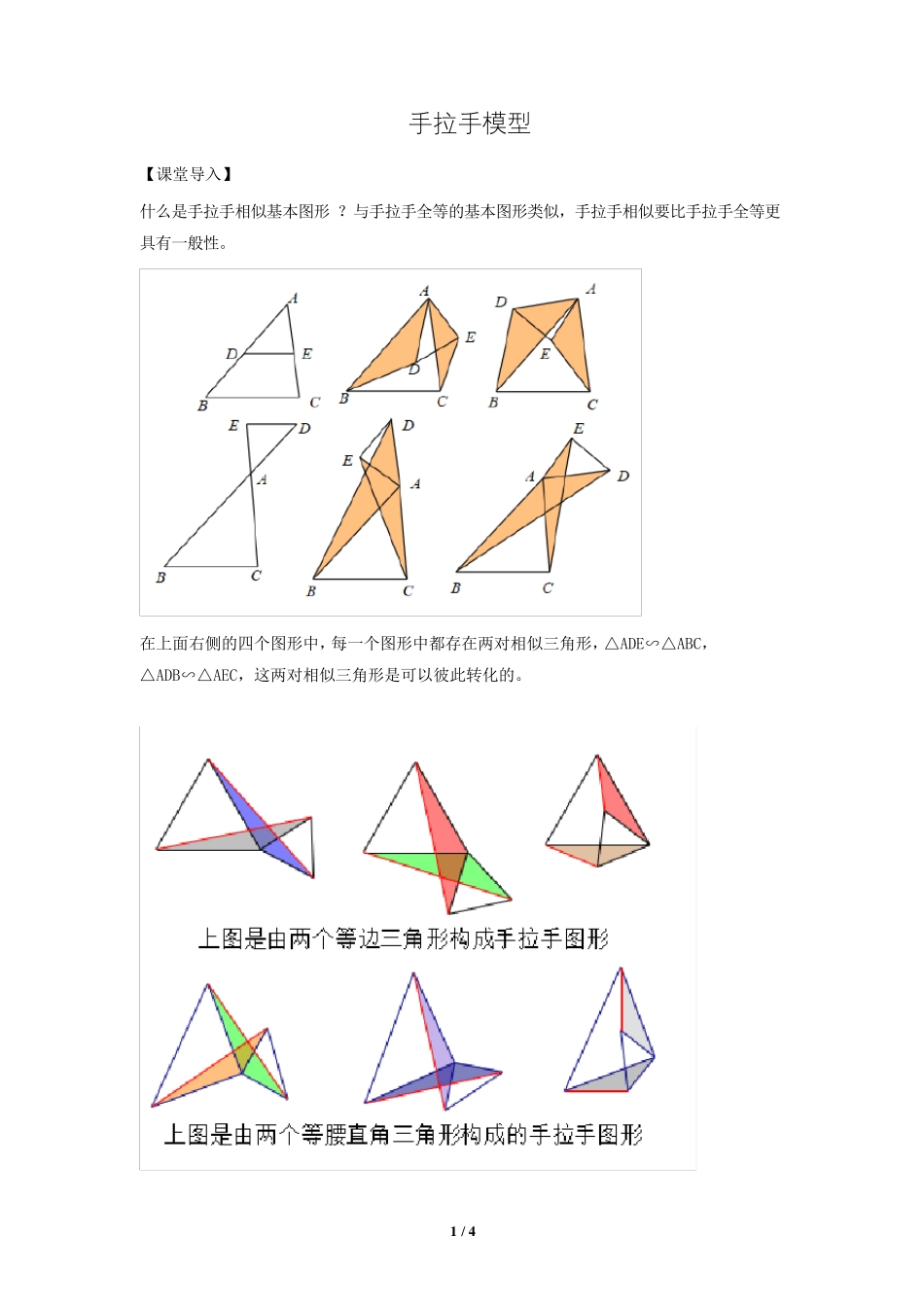
1 / 4 手 拉 手 模 型 【课堂导入】 什么是手拉手相似基本图形
与手拉手全等的基本图形类似，手拉手相似要比手拉手全等更具有一般性
在上面右侧的四个图形中，每一个图形中都存在两对相似三角形，△ADE∽△ABC，△ADB∽△AEC，这两对相似三角形是可以彼此转化的
2 / 4 【例1】 已知：△ABC，△DEF 都是等边三角形，M 是 BC 与 EF 的中点，连接 AD，BE
（1）如图 1，当 EF 与 BC 在同一条直线上时，直接写出 AD 与 BE 的数量关系和位置关系； （2）△ABC 固定不动，将图 1 中的△DEF 绕点M 顺时针旋转 （ 0o ≤ ≤ 90o ）角，如图 2 所示，判断（1）中的结论是否仍然成立，若成立，请加以证明；若不成立， 说明理由； 【例2】 以平面上一点O 为直角顶点，分别画出两①如图 1，当点D、C 分别在 AO、BO 的延长线上时 EMFM ②如图 2，将图 1 中的△AOB 绕点 O 沿顺时针方向旋转60度 角，其他条件不变，判断EMFM 的值是否发生变化，并对你的结论进行证明； 3 / 4 【例3】 如图 1，在△ABC 中，∠ACB=90°，BC=2，∠A=30°，点 E，F 分别是线段 BC，AC 的中点，连结 EF． （1）线段 BE 与 AF 的位置关系是_______， BEAF =_______． （2）如图 2，当△CEF 绕点 C 顺时针旋转α时（0°＜α＜18， 【例4】 如图 1，在四边形 ABCD 中，点 E、F 分别是 AB、CD 的中点，过点 E 作 AB 的垂线，过点 F 作 CD 的垂线，两垂线交于点G，连接 AG、BG、CG、DG，且∠AGD=∠BGC． （1） 求证：AD=BC． （2） 求证：△AGD∽△EGF． （3） 如图 2，若 AD、BC 所在直 线互相垂直，求 EFAD
