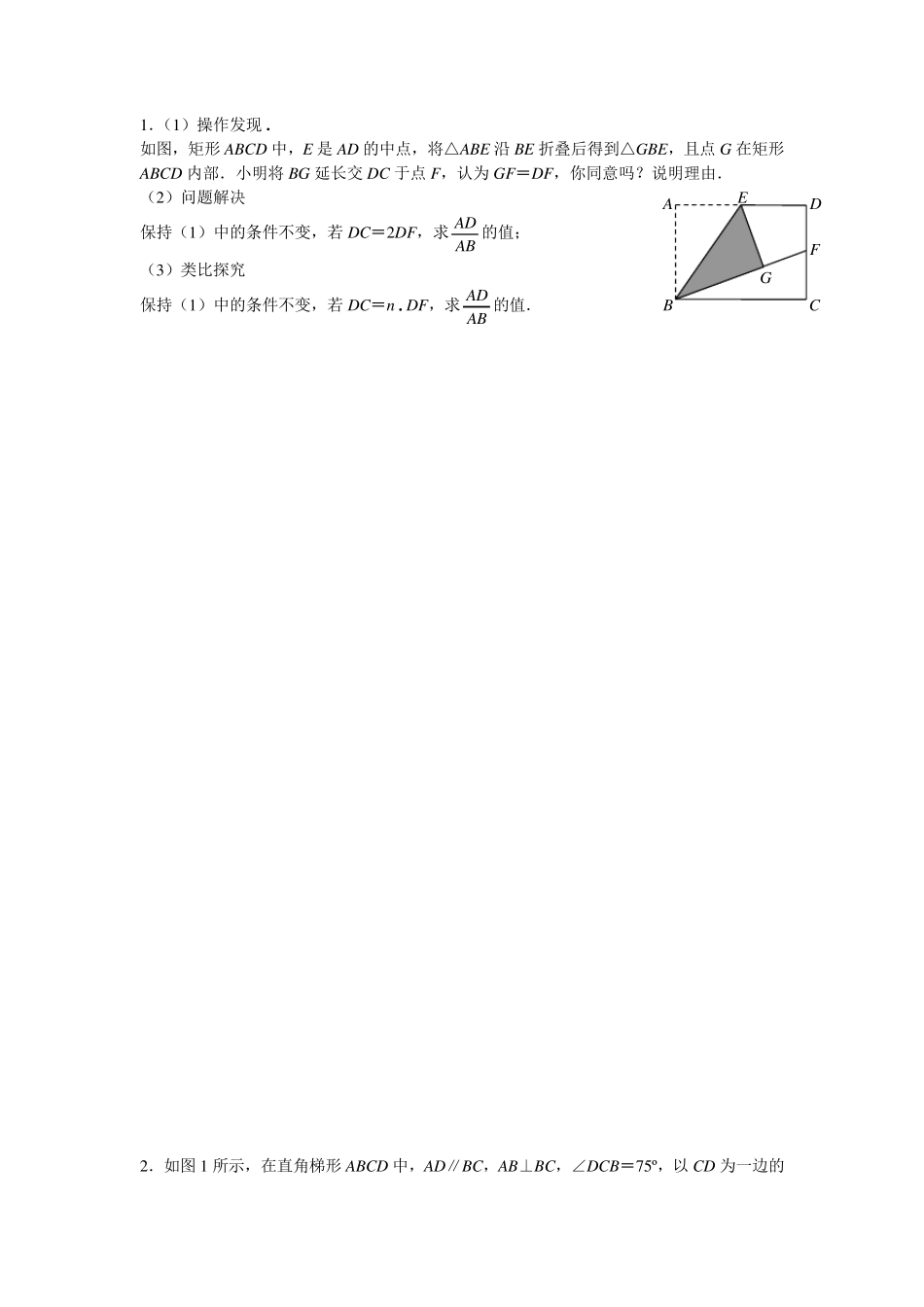
1.(1)操作发现· 如图,矩形 ABCD 中,E 是 AD 的中点,将△ABE 沿 BE 折叠后得到△GBE,且点 G 在矩形ABCD 内部.小明将 BG 延长交 DC 于点 F,认为 GF=DF,你同意吗?说明理由. (2)问题解决 保持(1)中的条件不变,若 DC=2DF,求ABAD 的值; (3)类比探究 保持(1)中的条件不变,若 DC=n·DF,求ABAD 的值. 2.如图 1 所示,在直角梯形 ABCD 中,AD∥BC,AB⊥BC,∠DCB=75º,以 CD 为一边的G B C E F A D 等边△DCE 的另一顶点E 在腰AB 上. (1)求∠AED 的度数; (2)求证:AB=BC; (3)如图 2 所示,若 F 为线段 CD 上一点,∠FBC=30º. 求 DFFC 的值. 3.如图①,在等腰梯形 ABCD 中,AD∥BC,AE⊥BC 于点E,DF⊥BC 于点F.AD=2cm,BC=6cm,AE=4cm.点P、Q 分别在线段 AE、DF 上,顺次连接 B、P、Q、C,线段 BP、PQ、QC、CB 所围成的封闭图形记为 M.若点P 在线段 AE 上运动时,点Q 也随之在线段DF 上运动,使图形 M 的形状发生改变,但面积始终..为 10cm2.设 EP=x cm,FQ=y cm,A B C D E 图 1 A B C D E 图 2 F 解答下列问题: (1 )直接写出当x=3 时y的值; (2 )求y与x之间的函数关系式,并写出自变量x的取值范围; (3 )当x取何值时,图形M 成为等腰梯形?图形M 成为三角形? (4 )直接写出线段PQ 在运动过程中所能扫过的区域的面积. 4 .如图①,将一张矩形纸片对折,然后沿虚线剪切,得到两个(不等边)三角形纸片△ABC,△A1 B1 C1 . A B C D E F (备用图) A B C D E F Q P 图① 图 ① A B C A1 B1 C1 (1)将△ABC,△A1B1C1 如图②摆放,使点A1 与B 重合,点B1 在AC 边的延长线上,连接CC1 交BB1 于点E.求证:∠B1C1C=∠B1BC. (2)若将△ABC,△A1B1C1 如图③摆放,使点B1 与B 重合,点A1 在AC 边的延长线上,连接CC1 交A1B 于点F.试判断∠A1C1C 与∠A1BC 是否相等,并说明理由. 5.将一副三角尺如图拼接:含 30°角的三角尺(△ABC)的长直角边与含 45°角的三角尺(△ACD)的斜边恰好重合.已知 AB=32,P 是 AC 上的一个动点. (1)当点P 运动到∠ABC 的平分线上时,连接DP,求DP 的长; (2)当点P 在运动过程中出现 PD=BC 时,求此时∠PDA 的度数; (3)当点P 运动到什么位置时,以 D,P,B...