离散数学公式VIP免费

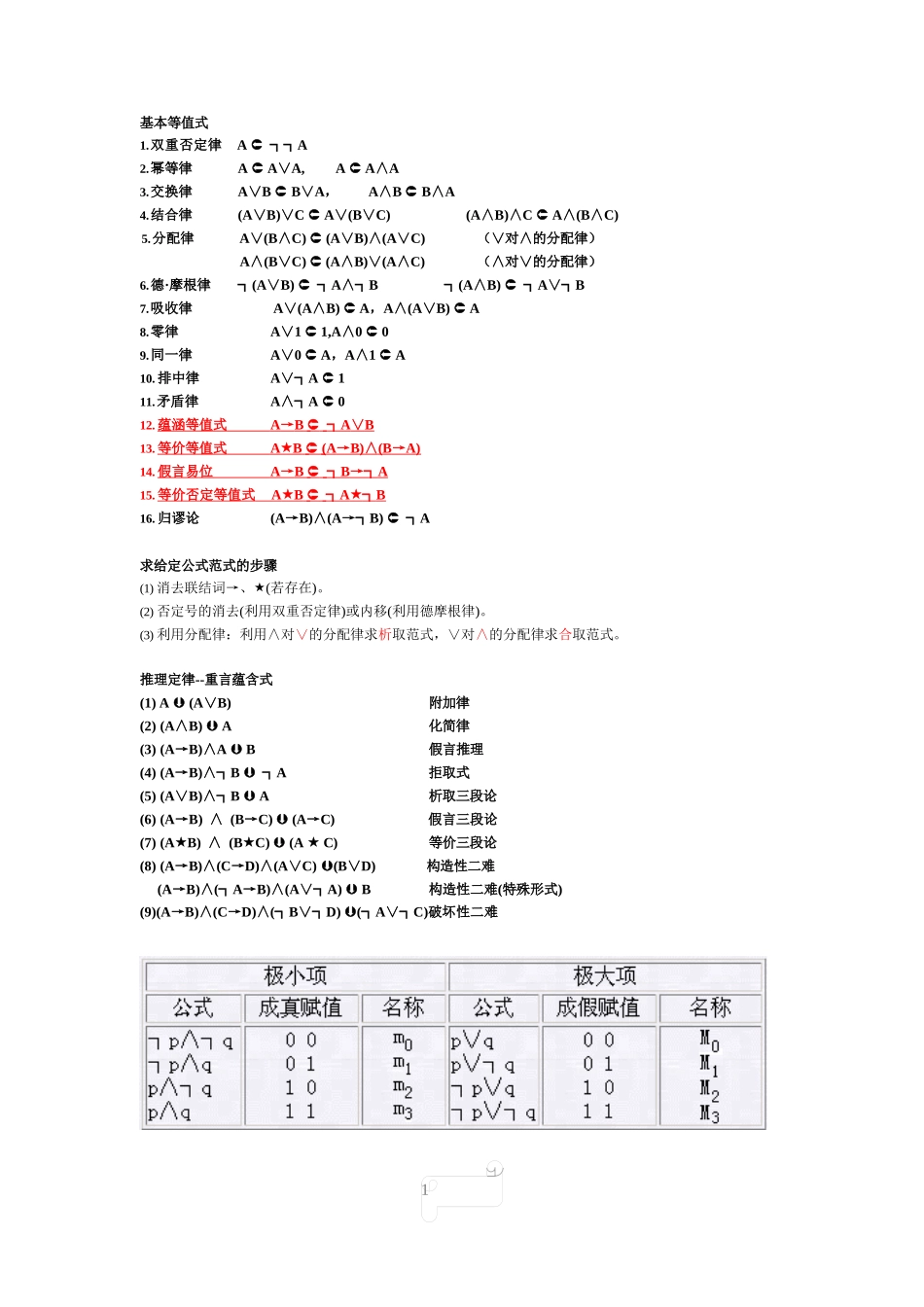
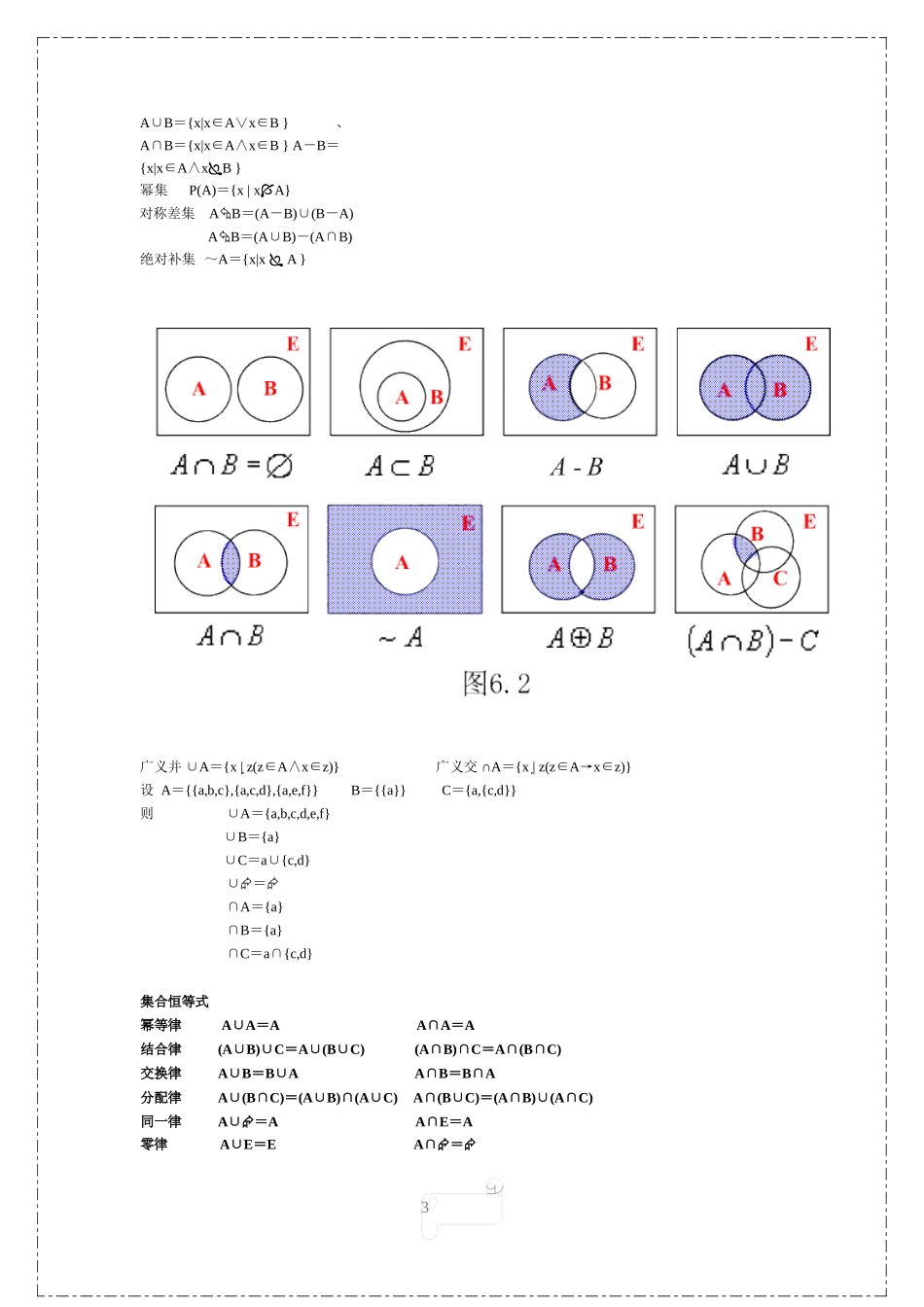
1基本等值式1.双重否定律 A  ┐┐A2.幂等律A  A∨A,A  A∧A3.交换律A∨B  B∨A，A∧B  B∧A4.结合律(A∨B)∨C  A∨(B∨C)(A∧B)∧C  A∧(B∧C)5.分配律A∨(B∧C)  (A∨B)∧(A∨C)（∨对∧的分配律）A∧(B∨C)  (A∧B)∨(A∧C)（∧对∨的分配律）6.德·摩根律┐(A∨B)  ┐A∧┐B┐(A∧B)  ┐A∨┐B7.吸收律A∨(A∧B)  A，A∧(A∨B)  A8.零律A∨1  1,A∧0  09.同一律A∨0  A，A∧1  A10. 排中律A∨┐A  111.矛盾律A∧┐A  012. 蕴涵等值 式 A → B  ┐ A ∨ B 13. 等价等值 式 A  B  (A → B) ∧ (B → A) 14. 假言易 位 A → B  ┐ B →┐ A 15. 等价否定等值式 A  B  ┐ A  ┐ B 16. 归谬论(A→B)∧(A→┐B)  ┐A求给定公式范式的步骤(1) 消去联结词→、(若存在)。(2) 否定号的消去(利用双重否定律)或内移(利用德摩根律)。(3) 利用分配律：利用∧对∨的分配律求析取范式，∨对∧的分配律求合取范式。推理定律--重言蕴含式(1) A  (A∨B)附加律(2) (A∧B)  A化简律(3) (A→B)∧A  B假言推理(4) (A→B)∧┐B  ┐A拒取式(5) (A∨B)∧┐B  A析取三段论(6) (A→B) ∧ (B→C)  (A→C)假言三段论(7) (AB) ∧ (BC)  (A  C)等价三段论(8) (A→B)∧(C→D)∧(A∨C) (B∨D)构造性二难(A→B)∧(┐A→B)∧(A∨┐A)  B构造性二难(特殊形式) (9)(A→B)∧(C→D)∧(┐B∨┐D) (┐A∨┐C)破坏性二难2SpongeBob SquarePants2设个体域为有限集 D={a1,a2,…,an},则有（1）xA(x)  A(a1)∧A(a2)∧…∧A(an)（2）xA(x)  A(a1)∨A(a2)∨…∨A(an)设 A(x)是任意的含自由出现个体变项 x 的公式，则（1┐） xA(x)  x┐A(x)（2┐） xA(x)  x┐A(x)设 A(x)是任意的含自由出现个体变项 x 的公式，B 中不含 x 的出现，则（1） x(A(x)∨B)  xA(x)∨Bx(A(x)∧B)  xA(x)∧Bx(A(x)→B)  xA(x)→Bx(B→A(x))  B→xA(x)（2） x(A(x)∨B)  xA(x)∨Bx(A(x)∧B)  xA(x)∧Bx(A(x)→B)  xA(x)→Bx(B→A(x))  B→xA(x)设 A(x)，B(x)是任意的含自由出现个体变项 x 的公式，则（1）x(A(x)∧B(x))  xA(x)∧xB(x)（2）x(A(x)∨B(x))  xA(x)...