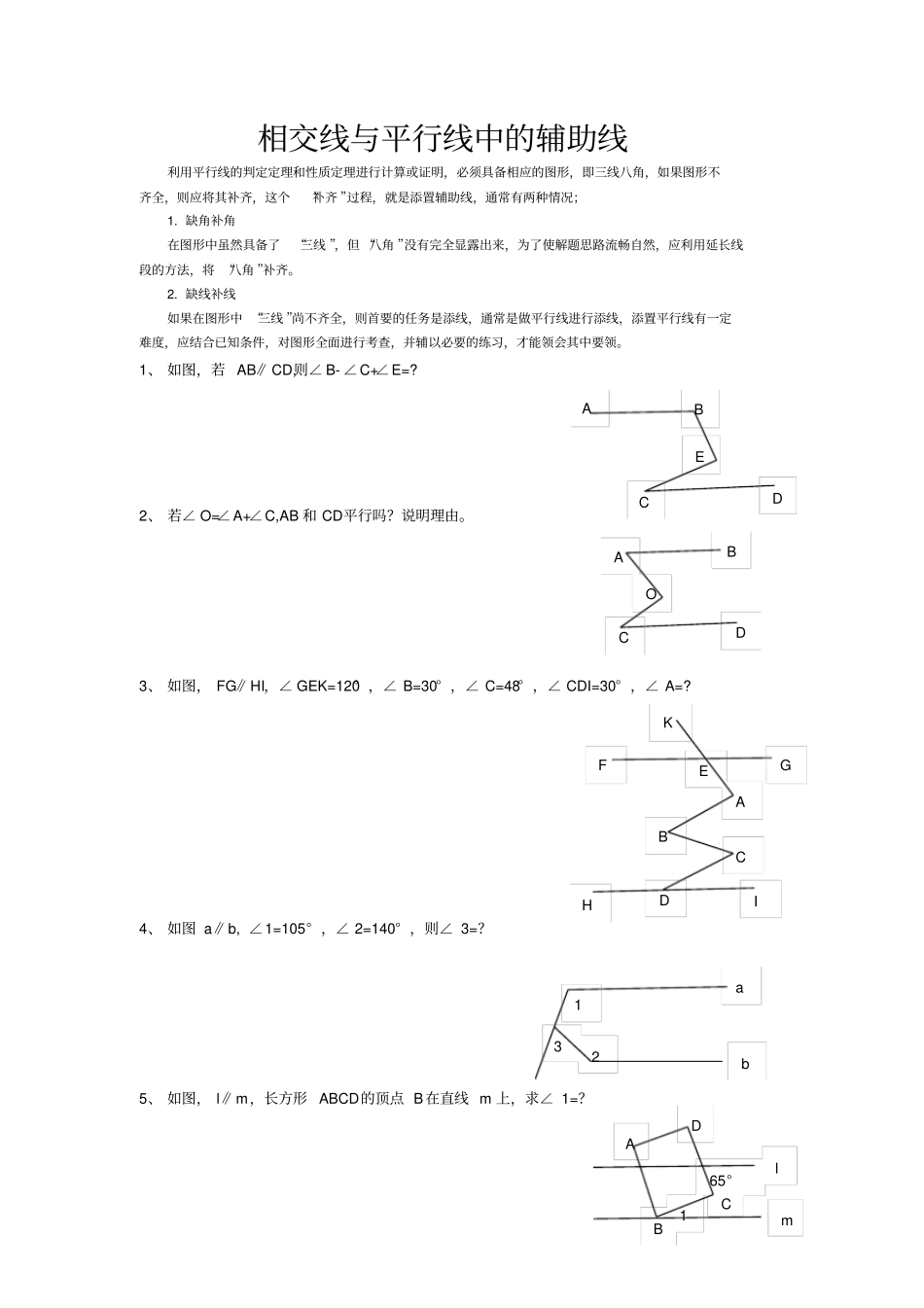
相交线与平行线中的辅助线利用平行线的判定定理和性质定理进行计算或证明,必须具备相应的图形,即三线八角,如果图形不齐全,则应将其补齐,这个“补齐 ”过程,就是添置辅助线,通常有两种情况;1. 缺角补角在图形中虽然具备了“三线 ”,但 “八角 ”没有完全显露出来,为了使解题思路流畅自然,应利用延长线段的方法,将 “八角 ”补齐。2. 缺线补线如果在图形中 “三线 ”尚不齐全,则首要的任务是添线,通常是做平行线进行添线,添置平行线有一定难度,应结合已知条件,对图形全面进行考查,并辅以必要的练习,才能领会其中要领。1、 如图,若 AB∥ CD,则∠ B- ∠C+∠E=? 2、 若∠ O=∠A+∠C,AB 和 CD平行吗?说明理由。3、 如图, FG∥HI,∠ GEK=120° ,∠ B=30° ,∠ C=48° ,∠ CDI=30° ,∠ A=? 4、 如图 a∥b, ∠1=105° ,∠ 2=140° ,则∠ 3=?5、 如图, l∥m,长方形 ABCD的顶点 B在直线 m 上,求∠ 1=?E D C B A D C O B A K E G F I H D C B A b a 3 2 1 65°1 m l D C B A 6、 如图 CD∥EF, ∠F+∠C=∠ABC,求证 AB∥GF 7、如图, AB∥CD,猜想∠ BAP、∠ APC 、∠ PCD的数量关系,并说明理由. 8、如图, AB∥CD,点 E是线段 AC 上一点,猜想∠BAC、∠ CED和∠ CDE之间的数量关系. 9、如图, AB∥CD,∠ 1=50°,∠ 2=110 °,则∠ 310、如图,已知∠B=25° ,∠ BCD=45° ,∠ CDE=30° ,∠ E=10° 。求证: AB∥EF 11、如图, AB∥ED,α =∠A+∠E,β =∠B+∠C+∠D.证明:β=2αG F E D C B A D C P B A E D C B A 3 2 1 D C B A F E D C B A E D C B A 12、已知 MN∥l,∠ ABC=130° ,∠ 1=40° ,求证: AB⊥MN 13、如图,已知AB∥CD,直线 EF 分别交 AB,CD于 E,F,∠ BEF的角平分线与∠DFE的角平分线相交于点P,求证∠ P=90° 。14、如图,已知C是线段 AB上的一点, AD∥BE, ∠ADC=∠ ACD, ∠ BCE=∠BEC, 求证: DC⊥CE 15、如图直线AC∥BD,连接 AB,直线 AC,BD,及线段 AB 把平面分成1,2,3,4 四个部分,规定:线段上各点不属于任何部分,当动点 P落在某个部分时, 连接 PA,PB,构成∠ PAC, ∠APB, ∠PBD三个角。(1)当动点 P 落在第 1 部分时,求证∠APB=∠PAC+∠PBD (2) 当动点 P 落在第 2 部分时,∠ APB=∠PAC+∠PBD是否成立(3)当动点 P 落在第 3 部分时, 全面探究∠ PAC, ∠APB, ∠PBD之间的关系, 并写出动点P的具体位置和相应的结论,选择其中一种结论加以证明。1 F C D B A l N M P F E D C B A E D B C A C P D B A 1 3 2 4 C D B A 1 3 2 4 C D B A 1 3 2 4