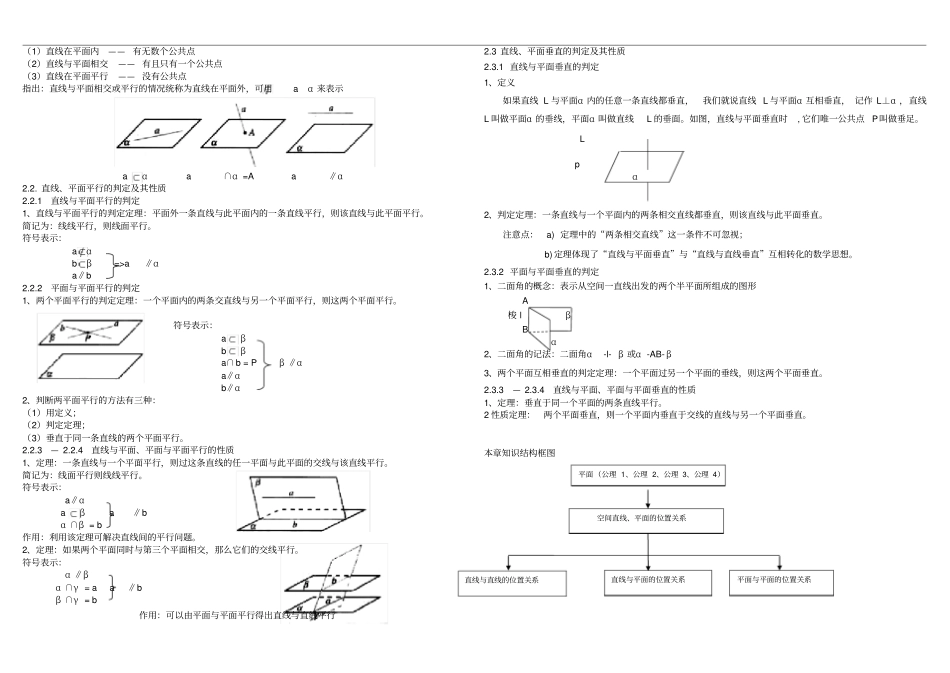
高中空间点线面之间位置关系知识点总结第一章空间几何体(一)空间几何体的结构特征(1)多面体——由若干个平面多边形围成的几何体. 旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。其中,这条定直线称为旋转体的轴。(2)柱,锥,台,球的结构特征1.1 棱柱——有两个面互相平行, 其余各面都是四边形, 并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。1.2 圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱. 2.1 棱锥——有一个面是多边形, 其余各面是有一个公共顶点的三角形, 由这些面所围成的几何体叫做棱锥。2.2 圆锥——以直角三角形的一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆锥。3.1 棱台——用一个平行于底面的平面去截棱锥,我们把截面与底面之间的部分称为棱台. 3.2 圆台——用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台. 4.1 球——以半圆的直径所在直线为旋转轴,半圆旋转一周形成的旋转体叫做球体,简称球. (二)空间几何体的三视图与直观图1. 投影:区分中心投影与平行投影。平行投影分为正投影和斜投影。2. 三视图——正视图;侧视图;俯视图;是观察者从三个不同位置观察同一个空间几何体而画出的图形;画三视图的原则:长对齐、高对齐、宽相等3. 直观图:直观图通常是在平行投影下画出的空间图形。4. 斜二测法:在坐标系' ''x o y 中画直观图时,已知图形中平行于坐标轴的线段保持平行性不变,平行于x轴(或在 x 轴上)的线段保持长度不变,平行于y 轴(或在 y 轴上)的线段长度减半。重点记忆:直观图面积 =原图形面积( 三) 空间几何体的表面积与体积1、空间几何体的表面积①棱柱、棱锥的表面积:各个面面积之和②圆柱的表面积③圆锥的表面积2Srlr④圆台的表面积22SrlrRlR⑤球的表面积24SR⑥扇形的面积公式213602n RSlr扇形(其中 l 表示弧长, r 表示半径)2、空间几何体的体积①柱体的体积VSh底②锥体的体积13VSh底③台体的体积1)3VSSSSh下下上上(④球体的体积343VR第二章直线与平面的位置关系2.1 空间点、直线、平面之间的位置关系2.1.1 1 平面含义:平面是无限延展的2 平面的画法及表示(1)平面的画法: 水平放置的平面通常画成一个平行四边形,锐角画成 450,且横边画成邻边的2 倍长(如图)(2)平面通常用希腊字母α...