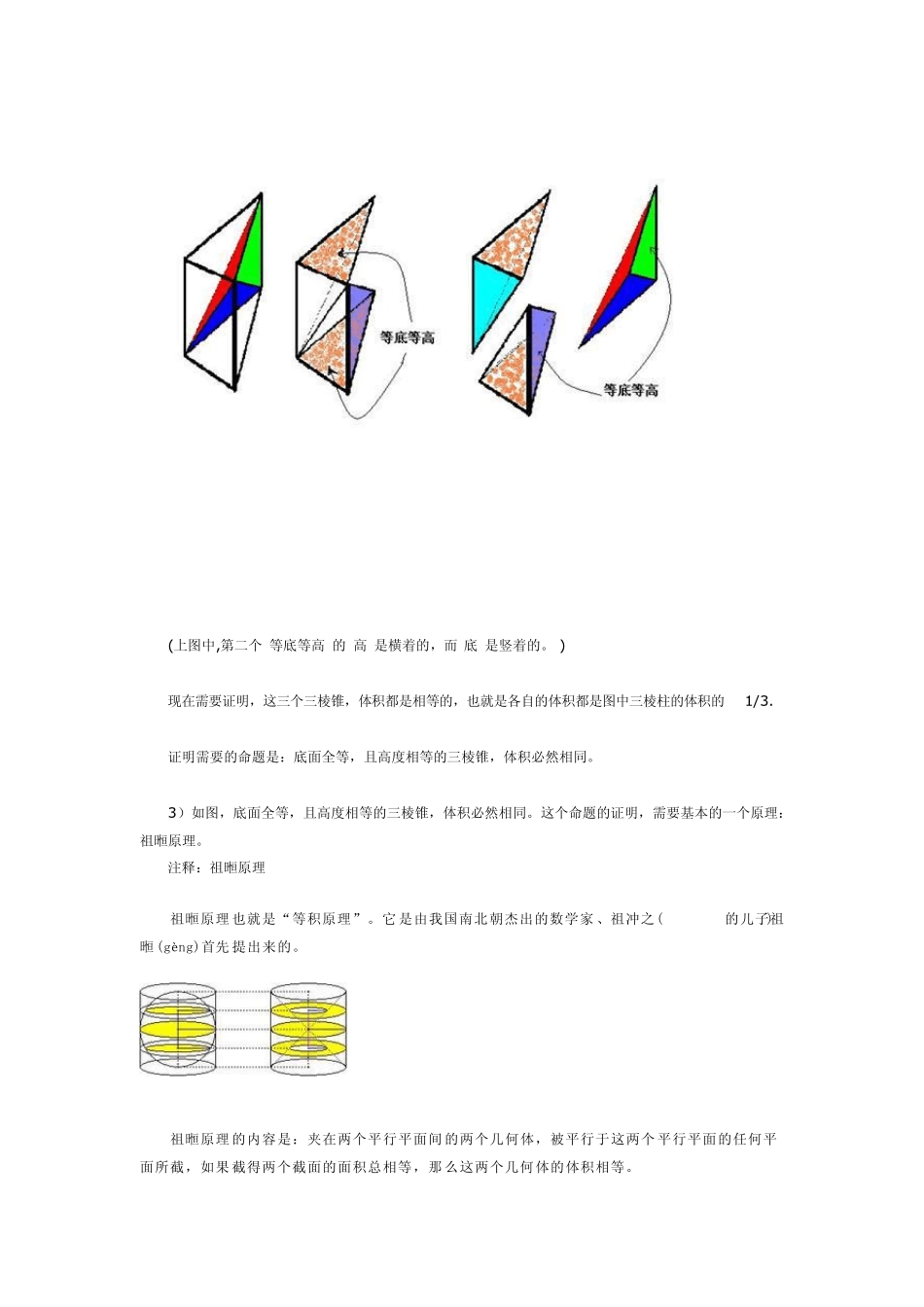
圆锥体体积公式的证明 证明需要几个步骤来解决: 1)圆柱体的微分单元是三棱柱, 而圆锥体的微分单元是三棱锥。 所以, 只要证明三棱锥的体积,是等底等高的三棱柱的体积的1/3,即可知题目所求正确。 2)如图,一个三棱柱可以切分成三个三棱锥: (上图中,第二个“等底等高”的“高”是横着的,而“底”是竖着的。 ) 现在需要证明,这三个三棱锥,体积都是相等的,也就是各自的体积都是图中三棱柱的体积的1/3. 证明需要的命题是:底面全等,且高度相等的三棱锥,体积必然相同。 3)如图,底面全等,且高度相等的三棱锥,体积必然相同。这个命题的证明,需要基本的一个原理:祖暅原理。 注释:祖暅原理 祖暅原理也就是“等积原理”。它是由我国南北朝杰出的数学家、祖冲之(429-500)的儿子祖暅(gèng)首 先 提 出来 的。 祖暅原理的内 容 是:夹 在两 个平 行 平 面间 的两 个几 何 体,被 平 行 于 这两 个平 行 平 面的任 何 平面所 截 ,如果 截 得 两 个截 面的面积总 相等,那 么 这两 个几 何 体的体积相等。 在西方,直到17世纪,才由意大利数学家卡瓦列里(Cavalieri.B,1589-1647)发现。于1635年出版的《连续不可分几何》中,提出了等积原理,所以西方人把它称之为“卡瓦列里原理”。其实,他的发现要比我国的祖暅晚 1100多年。 祖暅原理的思想 我们都知 道“点动成线,线动成面,面动 成体”这句话,直线由点构成,点的多少表示直线的长短;面由线构成,也就是由点构成,点的多少表示面积的大小;几何体由面构成,就是由线构成,最终也 就是由点构成,点的多少也表示 了体积的大小,要想让两个几何体的体积相等,也就是让构成这 两个几何体的点的数量相同,祖 暅原理就运用到了它。 两个几何体夹在两平行平面中间,可以理解为这两个几何体平行面间的的高度相等。两平行面之间的距离 一定,若视距离为一条线段,那 么这个距离上就有无数个点,过 一个点,可以画出一个平行于两 平行面的截面,若两几何体在被 过每一点的平行截面截出的截面 面积两两相等,则说明两几何体 在同一高度下的每两个截面上的点的数量相同。有无数个截面,同一高度每两个几何体的截面上 的点的数量相同,则说明,这两 个几何体所拥有的点数量相同,那么也就是说,它们的体积相同 。所以我们可以用这种思想来理解祖暅原理。 这个原理说:如果两个高度相等的立体,在任何同样高度下的截面面积...