圆锥曲线知识点+例题+练习含答案VIP免费

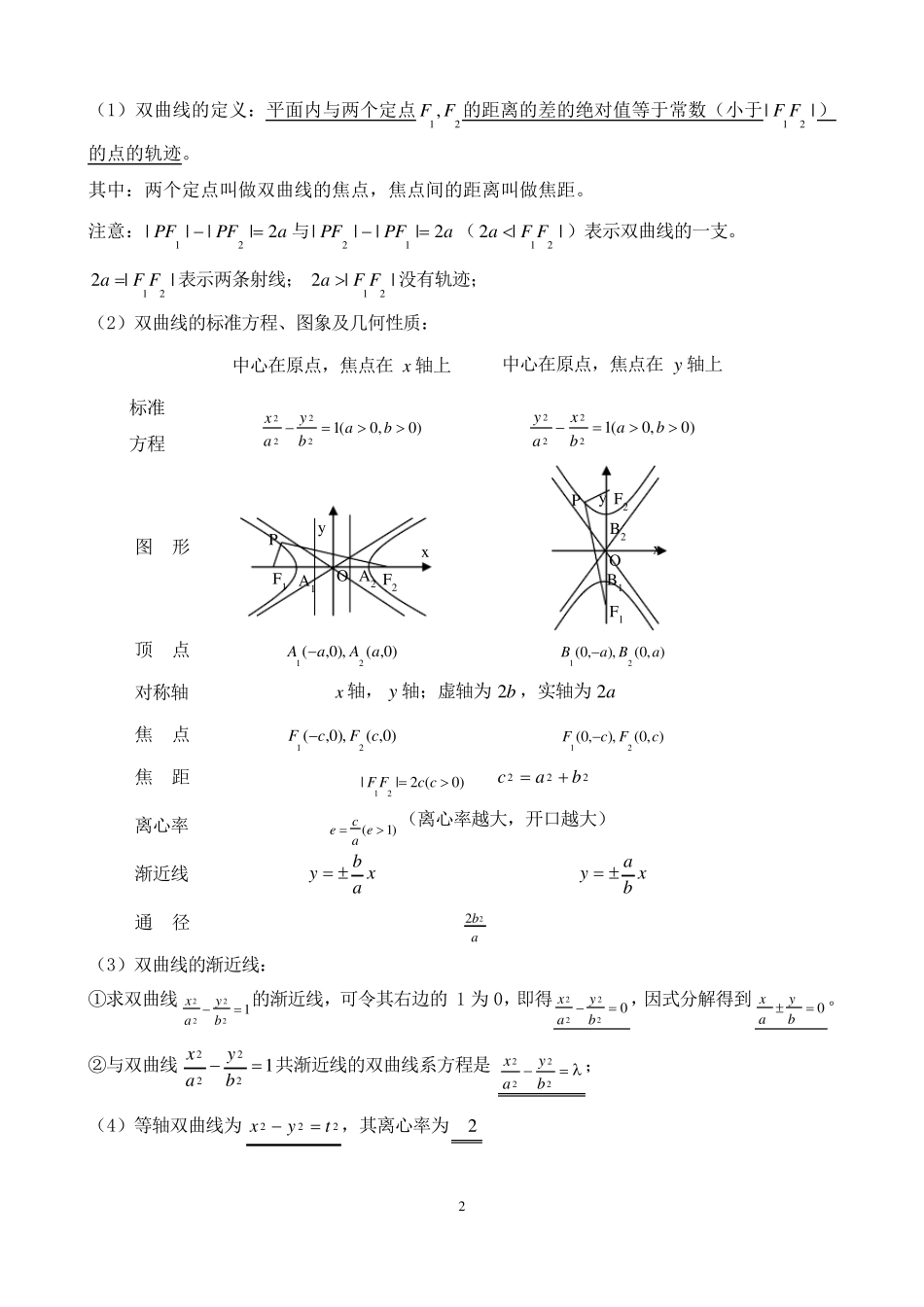
1 圆锥曲线 一、椭圆：（1）椭圆的定义：平面内与两个定点21, FF的距离的和等于常数（大于||21FF）的点的轨迹。 其中：两个定点叫做椭圆的焦点，焦点间的距离叫做焦距。 注意：||221FFa 表示椭圆；||221FFa 表示线段21FF；||221FFa 没有轨迹； （2）椭圆的标准方程、图象及几何性质： 中心在原点，焦点在x 轴上 中心在原点，焦点在y 轴上 标准方程 )0(12222babyax )0(12222babxay 图 形 顶 点 ),0(),,0()0,(),0,(2121bBbBaAaA ),0(),,0()0,(),0,(2121aBaBbAbA 对称轴 x轴， y 轴；短轴为 b2 ，长轴为 a2 焦 点 )0,(),0,(21cFcF  ),0(),,0(21cFcF 焦 距 )0(2||21ccFF 222bac 离心率 )10(eace（离心率越大，椭圆越扁） 通 径 22ba （过焦点且垂直于对称轴的直线夹在椭圆内的线段） 3．常用结论：（1）椭圆)0(12222babyax的两个焦点为21, FF，过1F 的直线交椭圆于BA,两点，则2ABF的周长= （2）设椭圆)0(12222babyax左、右两个焦点为21, FF，过1F 且垂直于对称轴的直线交椭圆于QP,两点，则QP,的坐标分别是 ||PQ 二、双曲线： x O F1 F2 P y A2 B2 B1 x O F1 F2 P y A2 A1 B1 B2 A1 2 （1）双曲线的定义：平面内与两个定点21, FF的距离的差的绝对值等于常数（小于||21FF）的点的轨迹。 其中：两个定点叫做双曲线的焦点，焦点间的距离叫做焦距。 注意：aPFPF2||||21与aPFPF2||||12（||221FFa ）表示双曲线的一支。 ||221FFa 表示两条射线；||221FFa 没有轨迹； （2）双曲线的标准方程、图象及几何性质： 中心在原点，焦点在x 轴上 中心在原点，焦点在y 轴上 标准 方程 )0,0(12222babyax )0,0(12222babxay 图 形 顶 点 )0,(),0,(21aAaA  ),0(),,0(21aBaB 对称轴 x 轴，y 轴；虚轴为b2 ，实轴为a2 焦 点 )0,(),0,(21cFcF  ),0(),,0(21cFcF 焦 距 )0(2||21ccFF 222bac 离心率 )1( eace（离心率越大，开口越大） 渐近线 xaby xbay 通 径 22ba （3）双曲线的渐近线： ①求双曲线12222 byax的渐近线，可令其右边的1 为0，即得02222 byax，因式分解得到0xyab 。 ②与双曲线12222byax共渐近线的双曲线系方程是2222byax； （4）等轴双曲线为222tyx，其离心率为2 ...