第五节振型向量正交性VIP免费

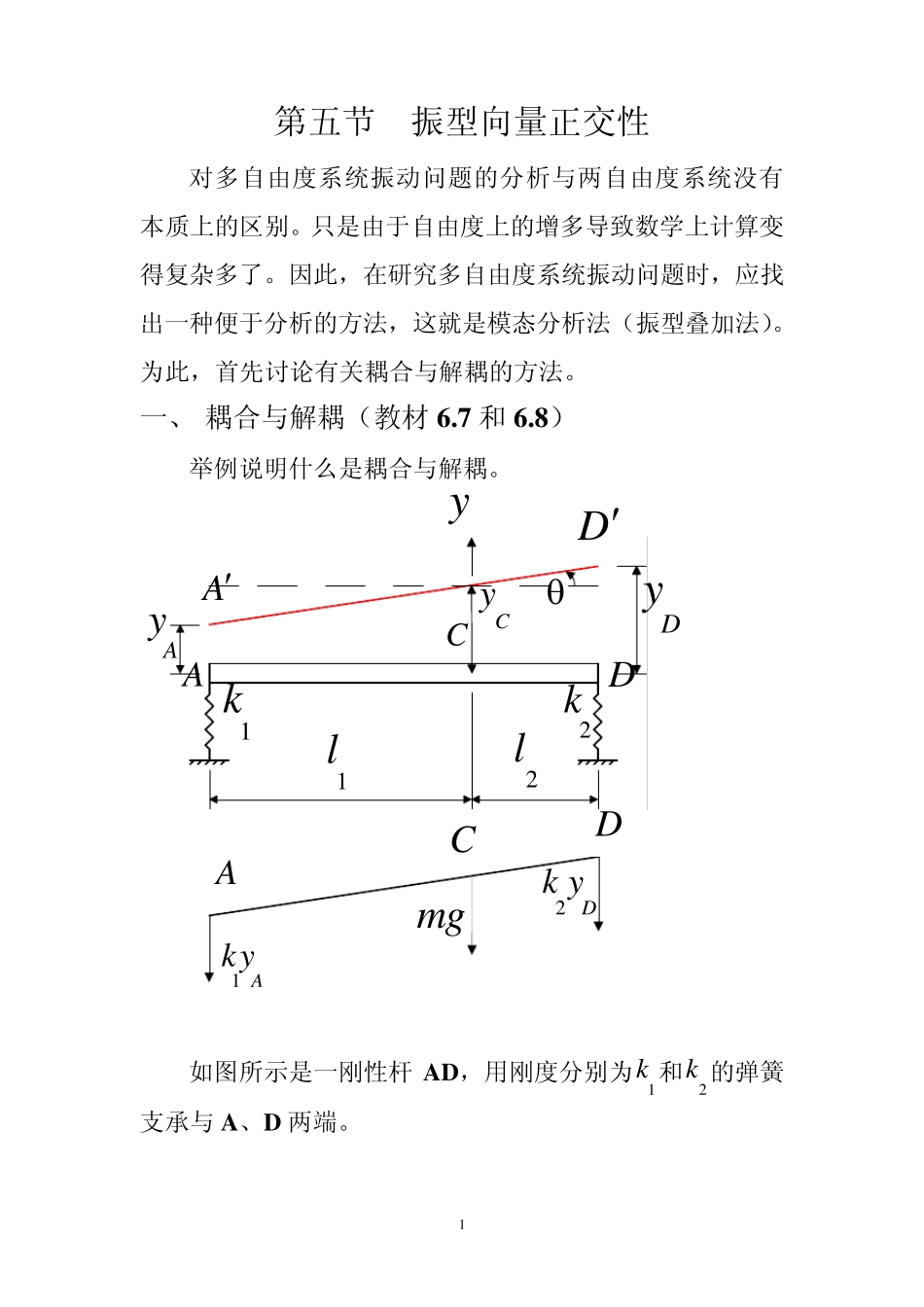
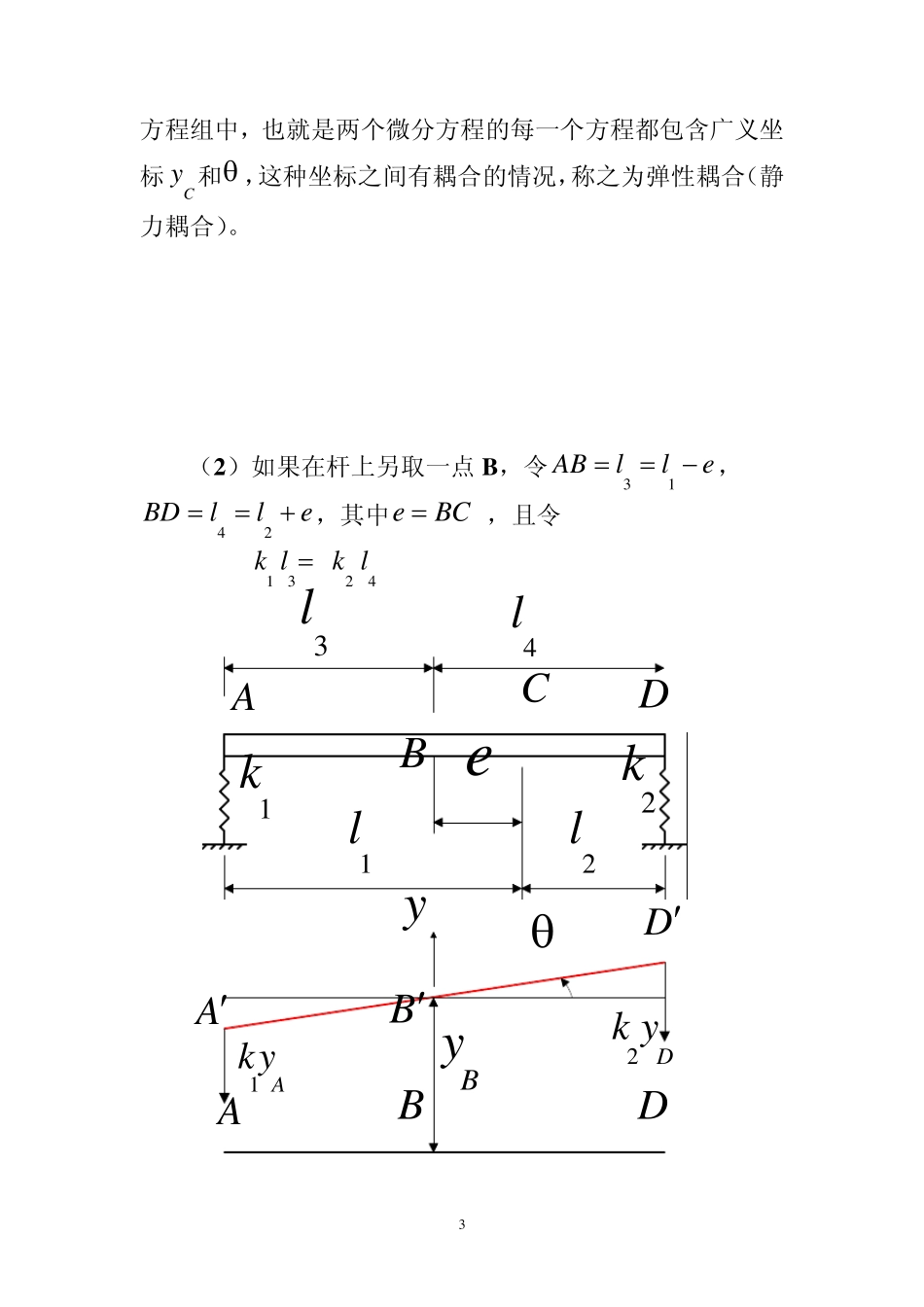
1 第五节 振型向量正交性 对多自由度系统振动问题的分析与两自由度系统没有本质上的区别。只是由于自由度上的增多导致数学上计算变得复杂多了。因此，在研究多自由度系统振动问题时，应找出一种便于分析的方法，这就是模态分析法（振型叠加法）。为此，首先讨论有关耦合与解耦的方法。 一、 耦合与解耦（教材 6.7 和 6.8） 举例说明什么是耦合与解耦。 .1l2l1k2k DDyCyAAyCy1AkyA2Dk ymgCDAD 如图所示是一刚性杆 A D ，用刚度分别为1k 和2k 的弹簧支承与A 、D 两端。 2 （1） 取质心C 点的垂直位移Cy 和刚性杆绕C 点的转角 为广义坐标。则刚性杆在振动中任一瞬时的受力如图所示。由几何关系，得 12112212DACACDCDAl yl yyyylllyylyyll 由牛顿运动定律，的系统的振动微分方程为 121122CADADmyk yk yJk y lk y l  （a） 式中 m 是刚性杆AD 的质量，J 是刚性杆AD 绕质心C 的转动惯量。整理式（a），得 122 21 1222 21 11 12 200CCCmykkyk lk lJk lk lyk lk l （b） 写成矩阵的形式 122 21 1222 21 11 12 20000CCykkk lk lymJk lk lk lk l     （c） 在上式中，质量矩阵是一个对角矩阵，反映在方程组中，就是两个微分方程的第一个方程仅包含一个广义坐标的二阶导数（加速度）Cy ，第二个方程仅包含另一个广义坐标的二阶导数 ，这种加速度（惯性力）之间没有耦合的情况，称之为惯性解耦。 刚度矩阵是非对角矩阵，反映在 3 方程组中，也就是两个微分方程的每一个方程都包含广义坐标Cy 和 ，这种坐标之间有耦合的情况，称之为弹性耦合（静力耦合）。 （2）如果在杆上另取一点 B ，令31ABlle， 42BDlle，其中eBC ，且令 1324k lk l .1l2l1k2kDAC1AkyA2Dk yD.eBBy3l4lByADB 4 以B 点的纵坐标By 和杆的转角 为广义坐标，则系统的振动微分方程为 122221 32 4()0()()0BBBmymekkymeyJmek lk l 写成矩阵形式 122221 32 40000BBykkmmeyk lk lmeJme     在新的坐标写出的...