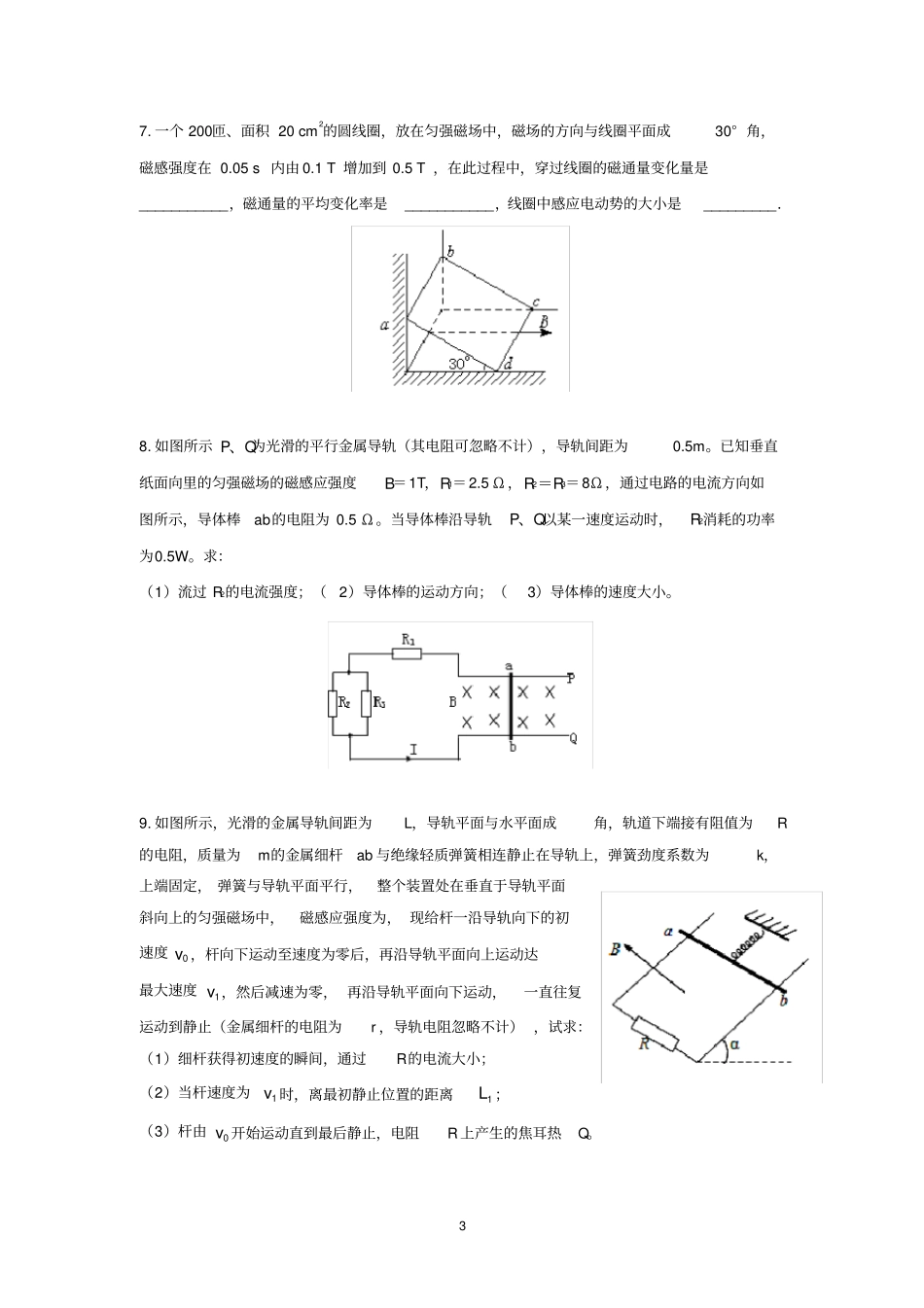
1 法拉第电磁感应定律及其应用专题训练计算题部分1. 如图所示, MN和 PQ为竖直方向的两平行长直金属导轨,间距 L 为 1m,电阻不计. 导轨所在的平面与磁感应强度B 为 1T 的匀强磁场垂直.质量m=0.2kg 、电阻 r =1Ω 的金属杆ab 始终垂直于导轨并与其保持光滑接触,导轨的上端有阻值为R=3Ω 的灯泡. 金属杆从静止下落,当下落高度为h=4m后灯泡保持正常发光. 重力加速度为g=10m/s2.求:(1)灯泡的额定功率;(2)金属杆从静止下落4m的过程中通过灯泡的电荷量;(3)金属杆从静止下落4m的过程中所消耗的电能2. 如图所示,两根足够长的光滑直金属导轨MN、PQ平行固定在倾角θ =37° 的绝缘斜面上,两导轨间距L=1m,导轨的电阻可忽略.M、P两点间接有阻值为R的电阻.一根质量m=1kg、电阻 r =0.2 Ω 的均匀直金属杆ab 放在两导轨上,与导轨垂直且接触良好.整套装置处于磁感应强度 B=0.5T 的匀强磁场中, 磁场方向垂直斜面向下.自图示位置起, 杆 ab 受到大小为F=0.5 v+2(式中 v 为杆 ab 运动的速度,力F 的单位为 N)、方向平行导轨沿斜面向下的拉力作用,由静止开始运动, 测得通过电阻R的电流随时间均匀增大.g 取 10m/s2,sin37 ° =0.6 .(1)试判断金属杆ab 在匀强磁场中做何种运动,并请写出推理过程;(2)求电阻 R的阻值;(3)求金属杆ab 自静止开始下滑通过位移x=1m所需的时间 t.3. 如图,两根相距l = 0.4m、电阻不计的平行光滑金属导轨水平放置,一端与阻值R=0.15Ω 的电阻相连。 导轨 x>0 一侧存在沿x 方向均匀增大的稳恒磁场,其方向与导轨平面垂直,变化率 k=0.5T/m ,x=0 处磁场的磁感应强度B0=0.5T 。一根质量 m=0.1kg 、电阻 r=0.05Ω 的金属棒置于导轨上,并与导轨垂直。棒在外力作用下从x=0 处以初速度v0=2m/s 沿导轨向右运动,运动过程中电阻上消耗的功率不变。求:(1)电路中的电流;(2)金属棒在x=2m处的速度;(3)金属棒从 x=0 运动到 x= 2m过程中安培力做功的大小;(4)金属棒从x=0 运动到 x=2m过程中外力的平均功率2 4. 如图甲所示,一个圆形线圈的匝数n=1000,面积 S=200cm2,电阻 r =1Ω ,在线圈外接一个阻值 R=4Ω 的电阻,电阻的一端b与地相接,把线圈放入一个方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间变化的规律如图乙所示.试问(1)0~4s 内,回路中的感应电动势;(2)从计时起,t =3s时...