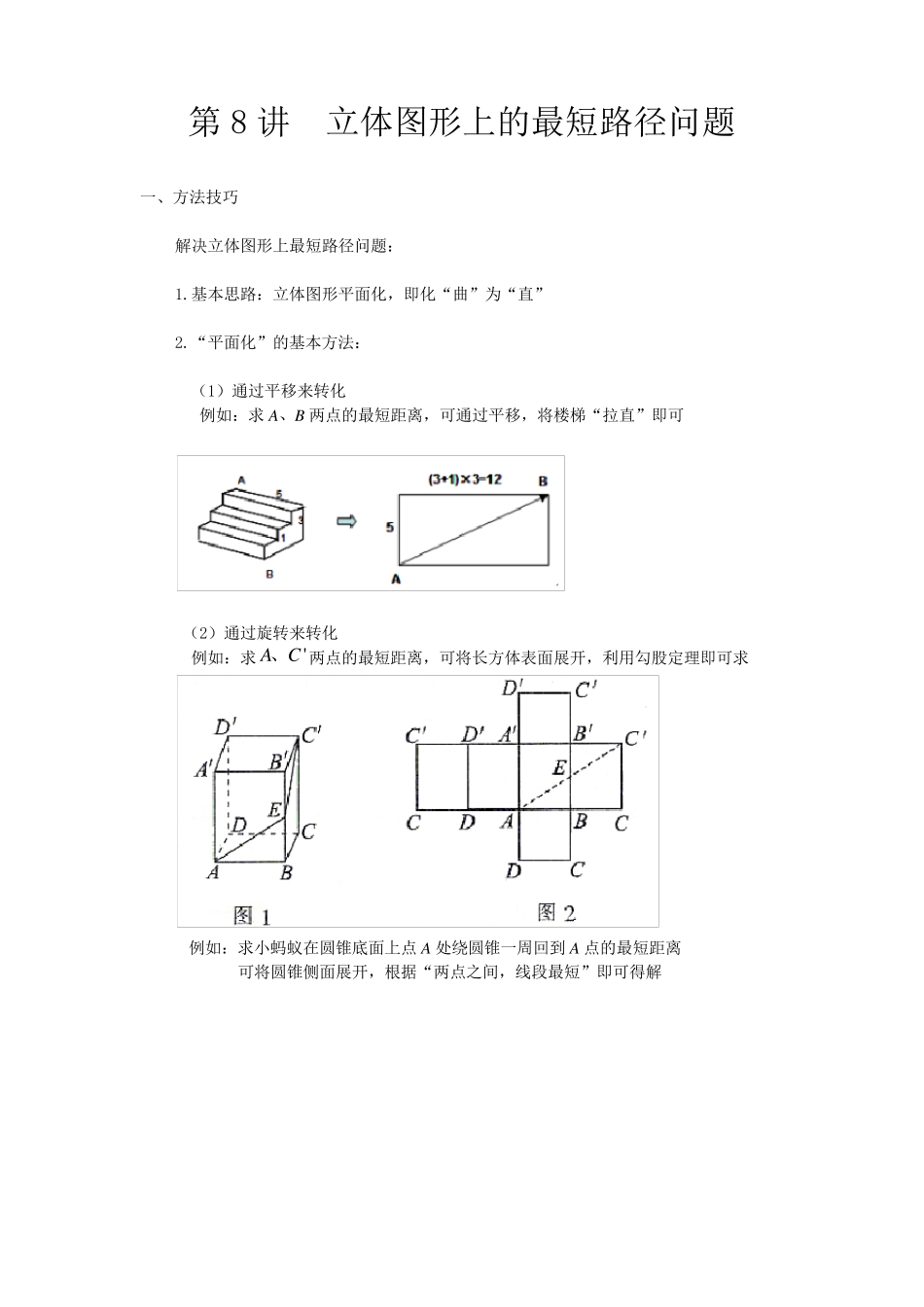
第8 讲 立体图形上的最短路径问题 一、方法技巧 解决立体图形上最短路径问题: 1.基本思路:立体图形平面化,即化“曲”为“直” 2.“平面化”的基本方法: (1)通过平移来转化 例如:求 A、B 两点的最短距离,可通过平移,将楼梯“拉直”即可 (2)通过旋转来转化 例如:求'A C、两点的最短距离,可将长方体表面展开,利用勾股定理即可求 例如:求小蚂蚁在圆锥底面上点 A 处绕圆锥一周回到 A 点的最短距离 可将圆锥侧面展开,根据“两点之间,线段最短”即可得解 (3)通过轴对称来转化 例如:求圆柱形杯子外侧点B 到内侧点A 的最短距离,可将杯子(圆柱)侧面展开,作点A 关于杯口的对称点'A ,根据“两点之间,线段最短”可知'A B 即为最短距离 3.储备知识点:(1)两点之间,线段最短 (2)勾股定理 4.解题关键:准确画出立体图形的平面展开图 二、应用举例 类型一 通过平移来转化 【例题 1 】如图,是一个三级台阶,它的每一级的长、宽和高分别等于5 cm ,3 cm 和 1 cm ,A 和 B 是这个台阶的两个相对的端点,A 点上有一只蚂蚁,想要到B 点去吃可口的食物,请你想一想,这只蚂蚁从 A 点出发,沿着台阶面爬到B 点,最短线路是多少? 【答案】1 3 cm 【解析】 试题分析: 只需将其展开便可直观得出解题思路,将台阶展开得到的是一个矩形,蚂蚁要从B 点到A 点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案. 试题解析: 解:展开图如图所示,2251 21 3ABcm 所以,蚂蚁爬行的最短路线是1 3 cm 类型二 通过旋转来转化 【例题2 】如下图,正四棱柱的底面边长为5 cm ,侧棱长为8 cm ,一只蚂蚁欲从正四棱柱底面上的A 点沿棱柱侧面到点C’处吃食物,那么它需要爬行的最短路径的长是多少? 【答案】cm4 12 【解析】 试题分析: 解这类题应将立体图形展开,转化为平面图形,把空间两点的距离转化为平面上两点间的距离,利用“同一平面内两点间的最短路线是连接这两点的线段”进行计算. 试题解析: 解:如图1 ,设蚂蚁爬行的路径是AEC’(在面ADD’A’上爬行是一样的).将四棱柱剪开铺平使矩形AA’B’B 与 BB’C’C 相连,连接 AC’,使 E 点在 AC’上(如图2 ) )(4 1281 0')('2222cmCCBCABAC 所以这只蚂蚁爬行的最短路径长为cm4 12 【难度】一般 【例题3 】如下图所示,圆柱形玻璃容器高1 8 cm,底面周长为6...