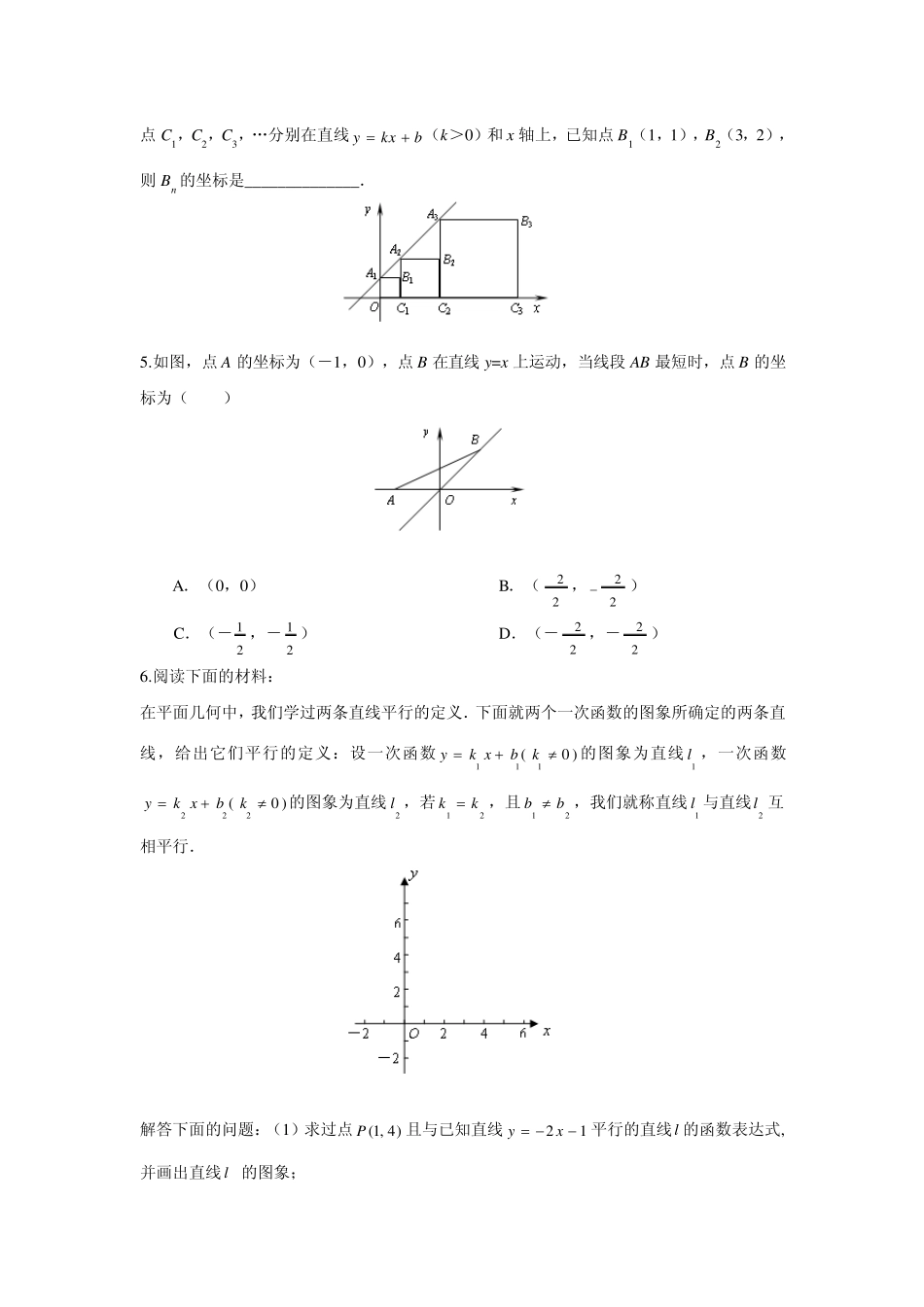
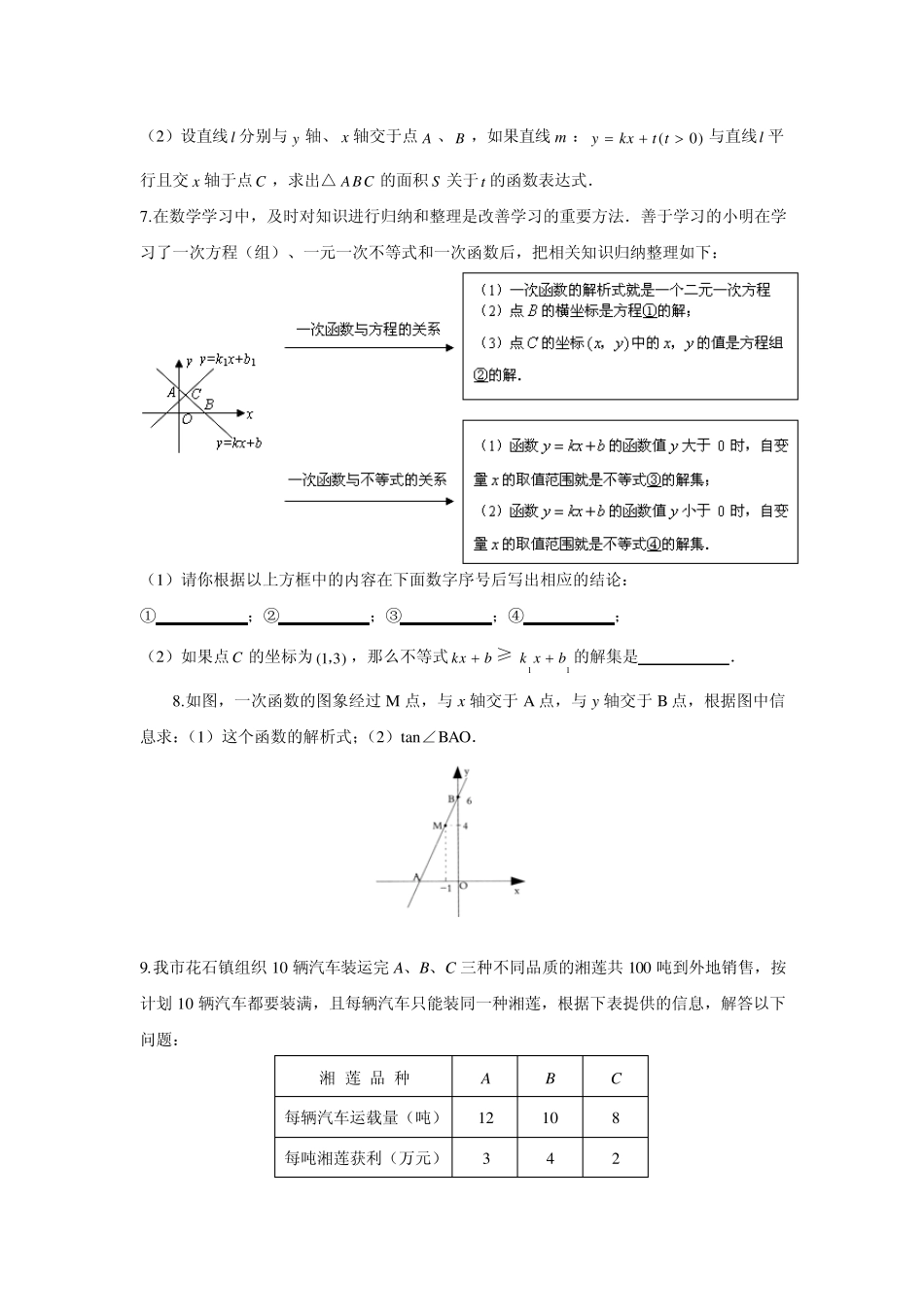
1.如图,在平面直角坐标系中,点 C(-3,0),点 A、B 分别在 x 轴、y 轴的正半轴上,且满足2310OBOA. (1)求点 A、点 B 的坐标; (2)若点P 从C点出发,以每秒1个单位的速度沿线段CB 由C向B 运动,连结AP,设ABP△的面积为 S,点 P 的运动时间为 t 秒,求 S 与 t 的函数关系式; (3)在(2)的条件下,是否存在点 P,使以点 A,B,P 为顶点的三角形与AOB△相似?若存在,请直接写出点 P 的坐标;若不存在,请说明理由. 2.如下图,直线 ykxb经过点( 12)A ,和点( 2 0)B , ,直线2yx过点 A,则不等式20xkxb的解集为( ) A.2x B.21x C.20x D.10x 3.某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱,供应这种纸箱有两种方案可供选择: 方案一:从纸箱厂定制购买,每个纸箱价格为 4 元; 方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000 元,每加工一个纸箱还需成本费2.4 元. (1)若需要这种规格的纸箱 x 个,请分别写出从纸箱厂购买纸箱的费用1y (元)和蔬菜加工厂自己加工制作纸箱的费用2y (元)关于x (个)的函数关系式; (2)假设你是决策者,你认为应该选择哪种方案?并说明理由. 4.正方形 A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点 A1,A2,A3,…和点C1,C2,C3,…分别在直线 ykxb(k>0)和 x 轴上,已知点B1(1,1),B2(3,2), 则 Bn 的坐标是______________. 5.如图,点A 的坐标为(-1,0),点B 在直线 y=x 上运动,当线段 AB 最短时,点B 的坐标为( ) A.(0,0) B.(22 ,22) C.(-21 ,-21 ) D.(-22 ,-22 ) 6.阅读下面的材料: 在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数111(0 )yk xbk的图象为直线1l ,一次函数222(0 )yk xbk的图象为直线2l ,若12kk,且12bb,我们就称直线1l 与直线2l 互相平行. 解答下面的问题:(1)求过点(1, 4)P且与已知直线21yx 平行的直线l 的函数表达式,并画出直线 l 的图象; (2)设直线l 分别与y 轴、x 轴交于点A 、B ,如果直线m :(0)ykxt t与直线...