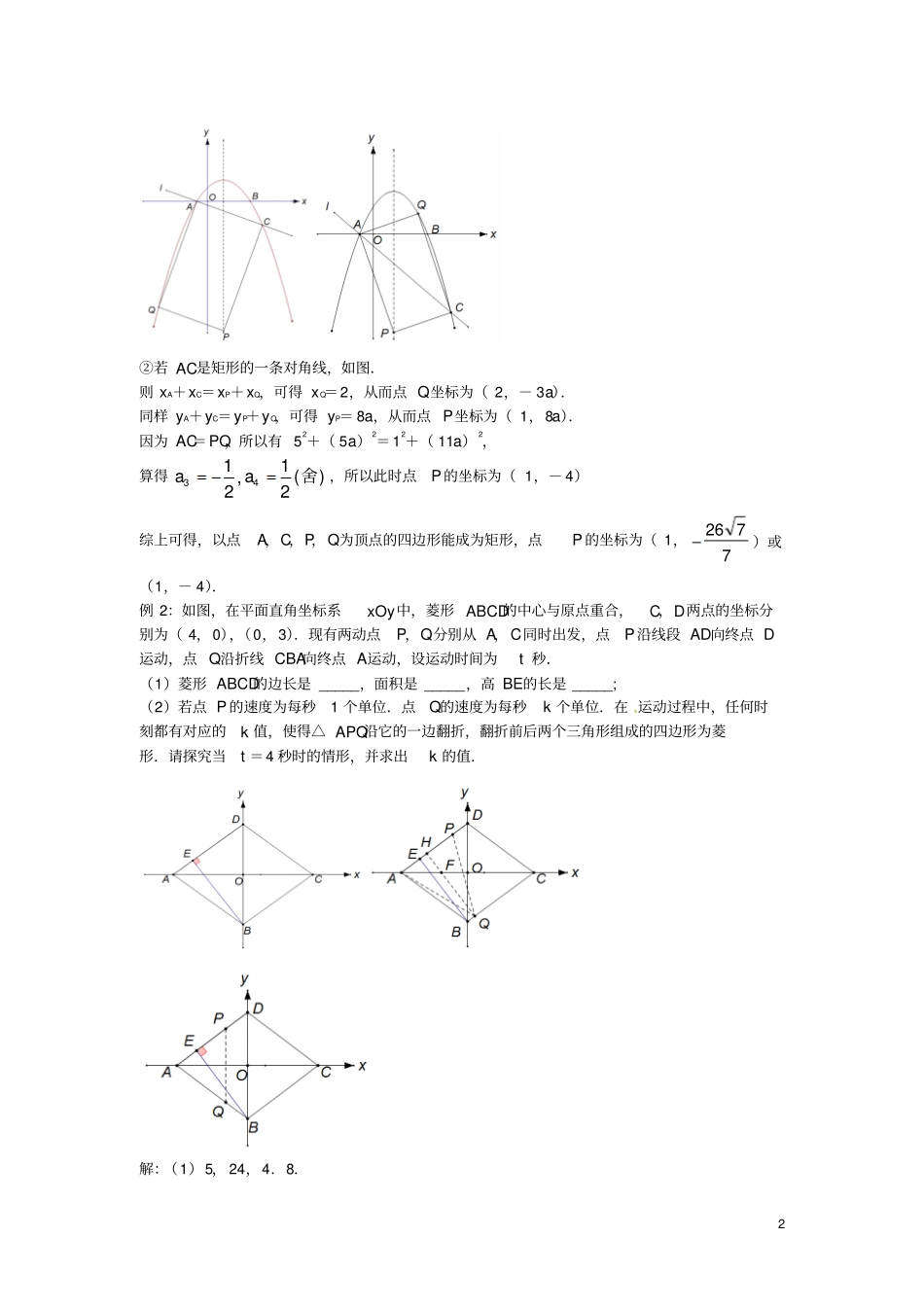
专题 24 特殊平行四边形的存在性破解策略在平行四边形的基础上增加一些条件,即可得到特殊的平行四边形因而可以结合”等腰三角形的存在性”,”直角三角形的存在性”和”平行四边形的存在性”来解决这类问题.例题讲解例 1:如图,在平面直角坐标系xOy中,抛物线y=ax2-2ax- 3a(a<0)与 x 轴交于 A,B两点(点 A在点 B 的左侧).经过点 A的直线 l :y=ax+a 与抛物线的另一交点为C,设 P是抛物线的对称轴上的一点,点Q在抛物线上,那么以点A,C, P,Q为顶点是四边形能否成为矩形 ?若能,求出点P 的坐标 ; 若不能,请说明理由.解:以点 A,C, P,Q为都顶点的四边形能成为矩形.令 ax2-2a-3a=ax+a.解得 x1=- 1,x2=4,所以点 A 的坐标为(- 1, 0),C的坐标为( 4,5a).因为 y= ax2-2ax-3a,所以抛物线的对称轴为x=1.则 xP=1.①若 AC是矩形的一条边,如图,则 xA+xP=xC+xQ,可得 xQ=- 4,从而点 Q坐标为(- 4,21a).同样 yA+yP=yC+yQ,可得 yP= 26a,从而点 P 坐标为( 1,26a).因为 AC=PQ,所以有 22+( 26a)2=82+( 16a)2,解得)(77,7721舍去aa,此时点 P 的坐标为( 1,7726)2②若 AC是矩形的一条对角线,如图.则 xA+xC=xP+xQ,可得 xQ=2,从而点 Q坐标为( 2,- 3a).同样 yA+yC=yP+yQ,可得 yP= 8a,从而点 P坐标为( 1,8a).因为 AC=PQ,所以有 52+( 5a)2=12+( 11a)2,算得)(21,2143舍aa,所以此时点P 的坐标为( 1,- 4)综上可得,以点A,C,P,Q为顶点的四边形能成为矩形,点P 的坐标为( 1,7726)或(1,- 4).例 2:如图,在平面直角坐标系xOy中,菱形 ABCD的中心与原点重合,C,D两点的坐标分别为( 4,0),(0,3).现有两动点P,Q分别从 A,C同时出发,点P 沿线段 AD向终点 D运动,点 Q沿折线 CBA向终点 A运动,设运动时间为t 秒.(1)菱形 ABCD的边长是 _____,面积是 _____,高 BE的长是 _____; (2)若点 P 的速度为每秒1 个单位.点Q的速度为每秒k 个单位.在 运动过程中,任何时刻都有对应的k 值,使得△ APQ沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形.请探究当t =4 秒时的情形,并求出k 的值.解:(1)5, 24,4.8.3( 2)要使△ APQ沿它的一边翻折,翻折前后的两个三角形组成的四边形为菱形,根据轴对称的性质,翻折...