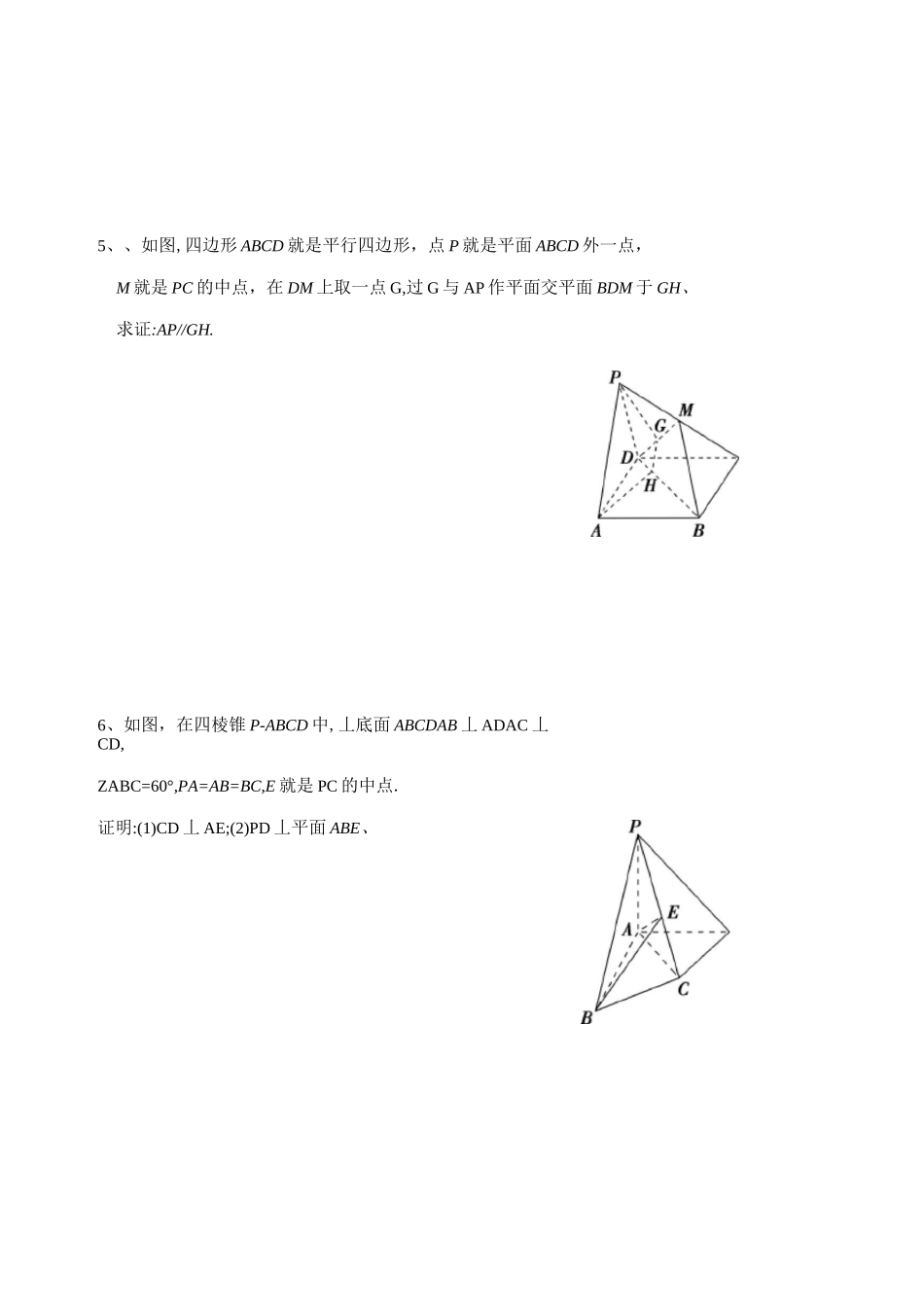
2020 届高三数学立体几何专题(文科)吴丽康 2019-111、如图,四棱锥 P-ABCD 中,底面 ABCD 为矩形,PA 丄平面 ABCD,E 为 PD 的点、(I)证明:PB//平面 AEC;(II)设 AP=1AD=3,三棱锥 P-ABD 的体积 V=1!,4求 A 点到平面 PBD 的距离、2、如图,四棱锥 P-ABCD 中,AB〃CDAB=2CD,E 为 PB 的中点.(1)求证:CE〃平面 PAD;(2)在线段 AB 上就是否存在一点 F,使得平面 PAD〃平面 CEF?若存在,证明您的结论,若不存在,请说明理由.PEPF =皿工 0).3 如图,在四棱锥 P—ABCD 中,平面 PAC 丄平面 ABCD,且 PA 丄 AC,PA=AD=2,四边形 ABCD 满足 BC^AD,AB 丄 ADAB=BC=1、点 E,F 分别为侧棱 PB,PC 上的点,(1)求证:EF〃平面 PAD;⑵ 当 A=1时,求点 D 到平面 AFB 的距离.4、如图,四棱柱 ABCD—A1B1C1D1的底面 ABCD 就是正方形.(1) 证明:平面 A]BD〃平面 CD1B1;(2) 若平面 ABCDn 平面 B1D1C=直线 l,证明:BD〃1、5、、如图,四边形 ABCD 就是平行四边形,点 P 就是平面 ABCD 外一点,M 就是 PC 的中点,在 DM 上取一点 G,过 G 与 AP 作平面交平面 BDM 于 GH、求证:AP//GH.6、如图,在四棱锥 P-ABCD 中,丄底面 ABCDAB 丄 ADAC 丄CD,ZABC=60°,PA=AB=BC,E 就是 PC 的中点.证明:(1)CD 丄 AE;(2)PD 丄平面 ABE、7、(2018 北京通州三模,18)如图,在四棱锥 P-ABCD 中,平面 PAB 丄平面 ABCD,四边形ABCD9、(2016-高考北京卷)如图,在四棱锥 P-ABCD 中,PC 丄平面 ABCDAB//DC,DC 丄 AC、11、如图,在四棱锥 P—ABCD 中,PA 丄平面 ABCD,FA=AB=BC^3,AD=CD=1,ZADC=120°,点 M 就是 AC 与 BD 的交点,点 N 在线段 PB 上,且 PN=*PB、(1) 证明:MN〃平面 PDC;(2) 求直线 MN 与平面 PAC 所成角的正弦值.12、(2016・高考四川卷)如图,在四棱锥 PABCD 中,PA 丄 CD,AD^BC,ZADC=ZP4B=90°,BC=CD^2AD.(1) 在平面 PAD 内找一点 M,使得直线 CM〃平面 P4B,并说明理由;(2) 证明:平面 PAB 丄平面 PBD.13.(2016・高考江苏卷)如图,在直三棱柱 ABCA1B1C1中,D,E 分别为 AB,BC的中点,点 F 在侧棱 BB 上,且 B]D 丄 A1F,A1C1±A1B1>求证:⑴ 直线 DE〃平面 A1C1F;(2)平面 B&E 丄平面 A&f、14、【2014,19】如图,三棱柱 ABC-ABC 中,111侧面 BBCC 为菱形,BC 的中点为 O,且 AO 丄平面 BBCC、11111(1)证明:BC 丄 AB;1⑵ 若 AC...