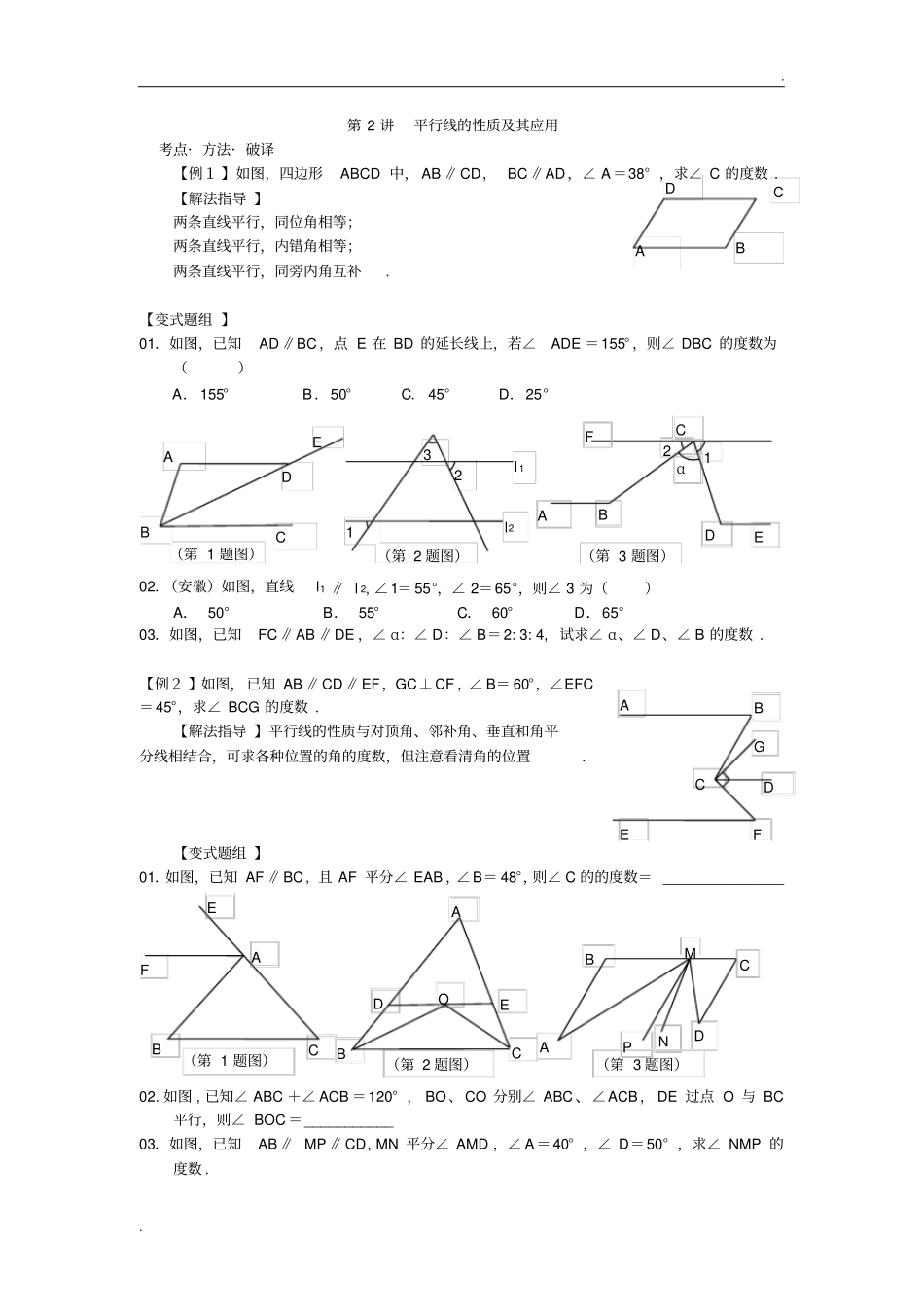
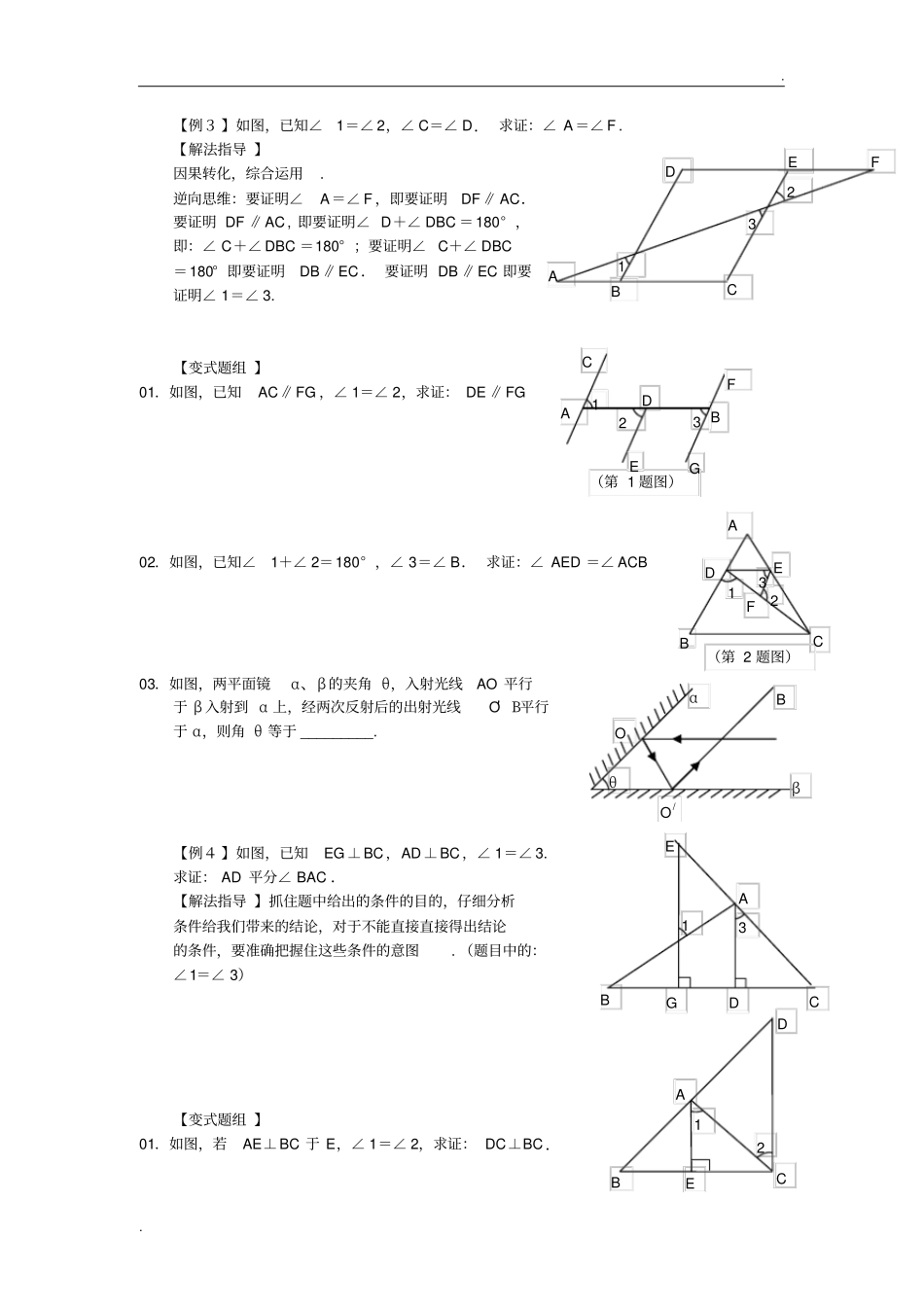
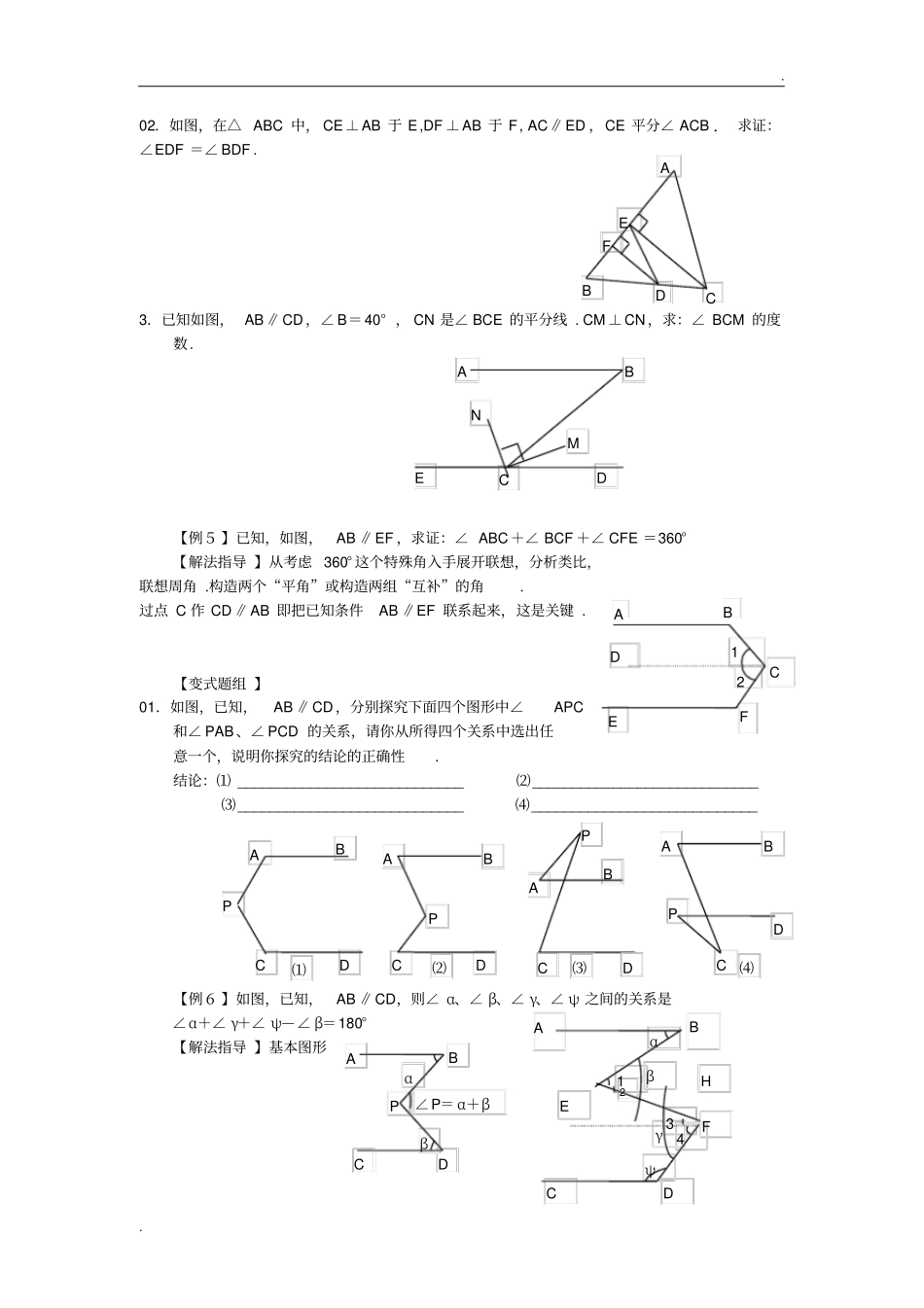
. . C B A D 第 2 讲平行线的性质及其应用考点· 方法· 破译【例1 】如图,四边形ABCD 中, AB ∥CD, BC∥AD,∠ A=38° ,求∠ C 的度数 . 【解法指导 】两条直线平行,同位角相等;两条直线平行,内错角相等;两条直线平行,同旁内角互补. 【变式题组 】01.如图,已知AD∥BC,点 E 在 BD 的延长线上,若∠ADE =155° ,则∠ DBC 的度数为()A. 155°B.50°C. 45°D.25°02.(安徽)如图,直线l1 ∥ l 2, ∠1= 55°,∠ 2=65°,则∠ 3 为()A. 50°B. 55°C. 60°D.65°03.如图,已知FC∥AB ∥DE ,∠ α:∠ D:∠ B=2: 3: 4, 试求∠ α、∠ D、∠ B 的度数 . 【例2 】如图,已知 AB ∥CD ∥EF,GC⊥CF ,∠ B= 60°,∠EFC=45°,求∠ BCG 的度数 .【解法指导 】平行线的性质与对顶角、邻补角、垂直和角平分线相结合,可求各种位置的角的度数,但注意看清角的位置. 【变式题组 】01.如图,已知 AF ∥BC, 且 AF 平分∠ EAB ,∠B= 48°,则∠ C 的的度数= _______________ 02. 如图 , 已知∠ ABC +∠ ACB =120° , BO 、CO 分别∠ ABC、∠ACB, DE 过点 O 与 BC平行,则∠ BOC =___________03.如图,已知AB∥ MP ∥CD, MN 平分∠ AMD ,∠ A=40° ,∠ D=50° ,求∠ NMP 的度数 .A B C D O E F A E B C (第 1 题图)(第 2 题图)E A B D α1 2 C F (第 3 题图)3 2 1 l 1l2(第 2 题图)(第 1 题图)E D C B A E A F G D C B B A M C D N P (第 3 题图). . D A 2 E 1 B C 【例3 】如图,已知∠1=∠ 2,∠ C=∠ D. 求证:∠ A=∠ F .【解法指导 】因果转化,综合运用. 逆向思维:要证明∠A=∠ F ,即要证明DF∥ AC.要证明 DF ∥AC, 即要证明∠ D+∠ DBC =180° ,即:∠ C+∠ DBC =180° ;要证明∠ C+∠ DBC =180° 即要证明DB∥EC. 要证明 DB ∥EC 即要证明∠ 1=∠ 3. 【变式题组 】01.如图,已知AC∥FG ,∠ 1=∠ 2,求证: DE ∥FG 02.如图,已知∠1+∠ 2=180° ,∠ 3=∠ B. 求证:∠ AED =∠ ACB03.如图,两平面镜α、β 的夹角 θ,入射光线AO 平行于 β 入射到 α 上,经两次反射后的出射光线O′ B平行于 α,则...