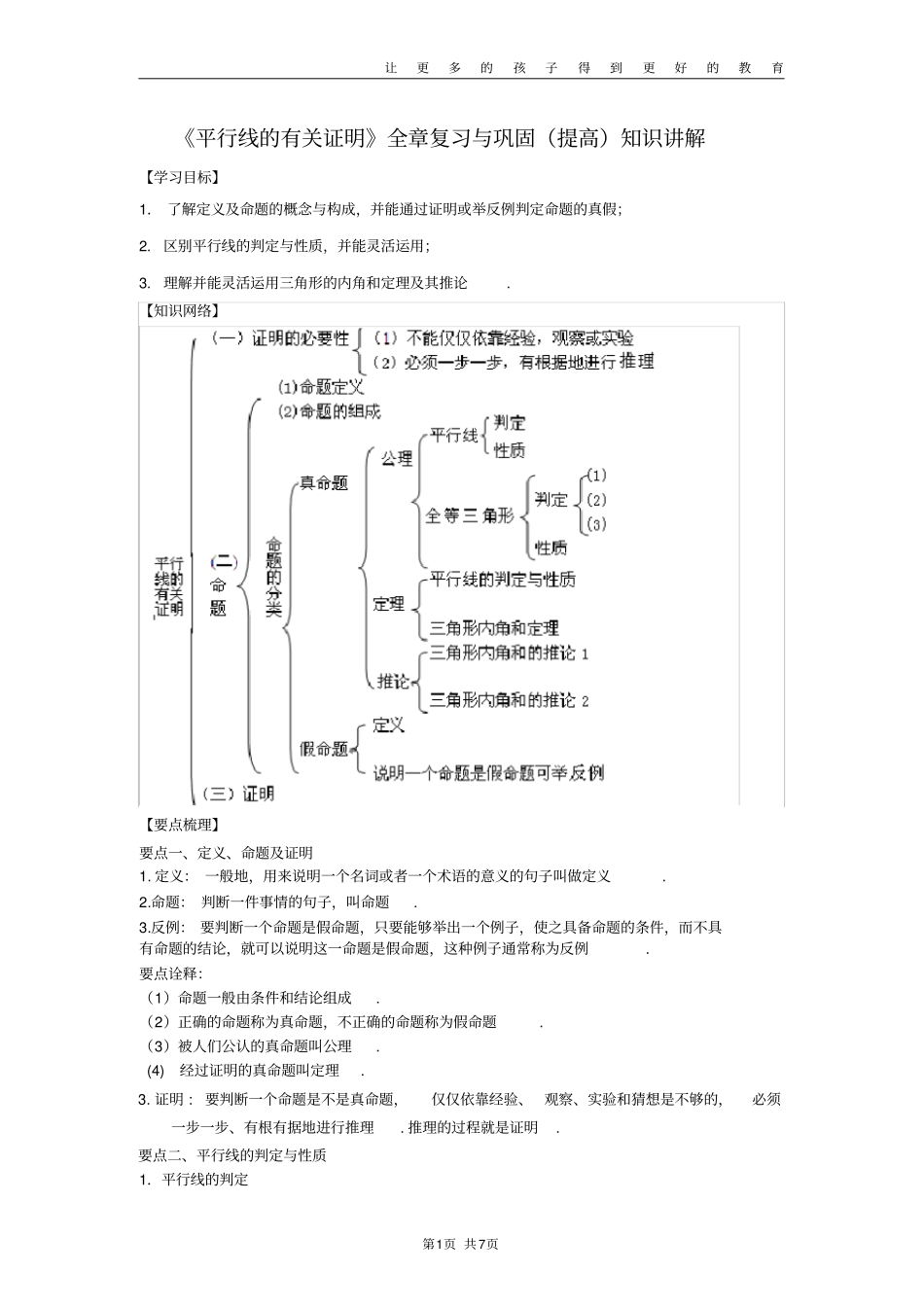
让更多的孩子得到更好的教育第1页 共 7页《平行线的有关证明》全章复习与巩固(提高)知识讲解【学习目标】1. 了解定义及命题的概念与构成,并能通过证明或举反例判定命题的真假;2. 区别平行线的判定与性质,并能灵活运用;3. 理解并能灵活运用三角形的内角和定理及其推论. 【知识网络】【要点梳理】要点一、定义、命题及证明1. 定义: 一般地,用来说明一个名词或者一个术语的意义的句子叫做定义.2.命题: 判断一件事情的句子,叫命题.3.反例: 要判断一个命题是假命题,只要能够举出一个例子,使之具备命题的条件,而不具有命题的结论,就可以说明这一命题是假命题,这种例子通常称为反例. 要点诠释:(1)命题一般由条件和结论组成.(2)正确的命题称为真命题,不正确的命题称为假命题.(3)被人们公认的真命题叫公理.(4) 经过证明的真命题叫定理.3. 证明 :要判断一个命题是不是真命题,仅仅依靠经验、 观察、实验和猜想是不够的,必须一步一步、有根有据地进行推理. 推理的过程就是证明. 要点二、平行线的判定与性质1.平行线的判定让更多的孩子得到更好的教育第2页 共 7页判定方法 1: 同位角相等,两直线平行.判定方法 2: 内错角相等,两直线平行.判定方法 3: 同旁内角互补,两直线平行.要点诠释: 根据平行线的定义和平行公理的推论,平行线的判定方法还有:(1)平行线的定义:在同一平面内,如果两条直线没有交点(不相交),那么两直线平行. (2)如果两条直线都平行于第三条直线,那么这两条直线平行(平行线的传递性). (3)在同一平面内,垂直于同一直线的两条直线平行. (4)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.2.平行线的性质性质 1:两直线平行,同位角相等;性质 2:两直线平行,内错角相等;性质 3:两直线平行,同旁内角互补. 要点诠释: 根据平行线的定义和平行公理的推论,平行线的性质还有:(1)若两条直线平行,则这两条直线在同一平面内,且没有公共点.(2)如果一条直线与两条平行线中的一条直线垂直,那么它必与另一条直线垂直.要点三、三角形的内角和定理及推论三角形的内角和定理:三角形的内角和等于180° .推论:(1)三角形的一个外角等于与它不相邻的两个内角的和.(2)三角形的一个外角大于与它不相邻的任何一个内角.要点诠释:(1)由一个公理或定理直接推出的真命题,叫做这个公理或定理的推论. (2)推论可以当做定理使用. 【典...