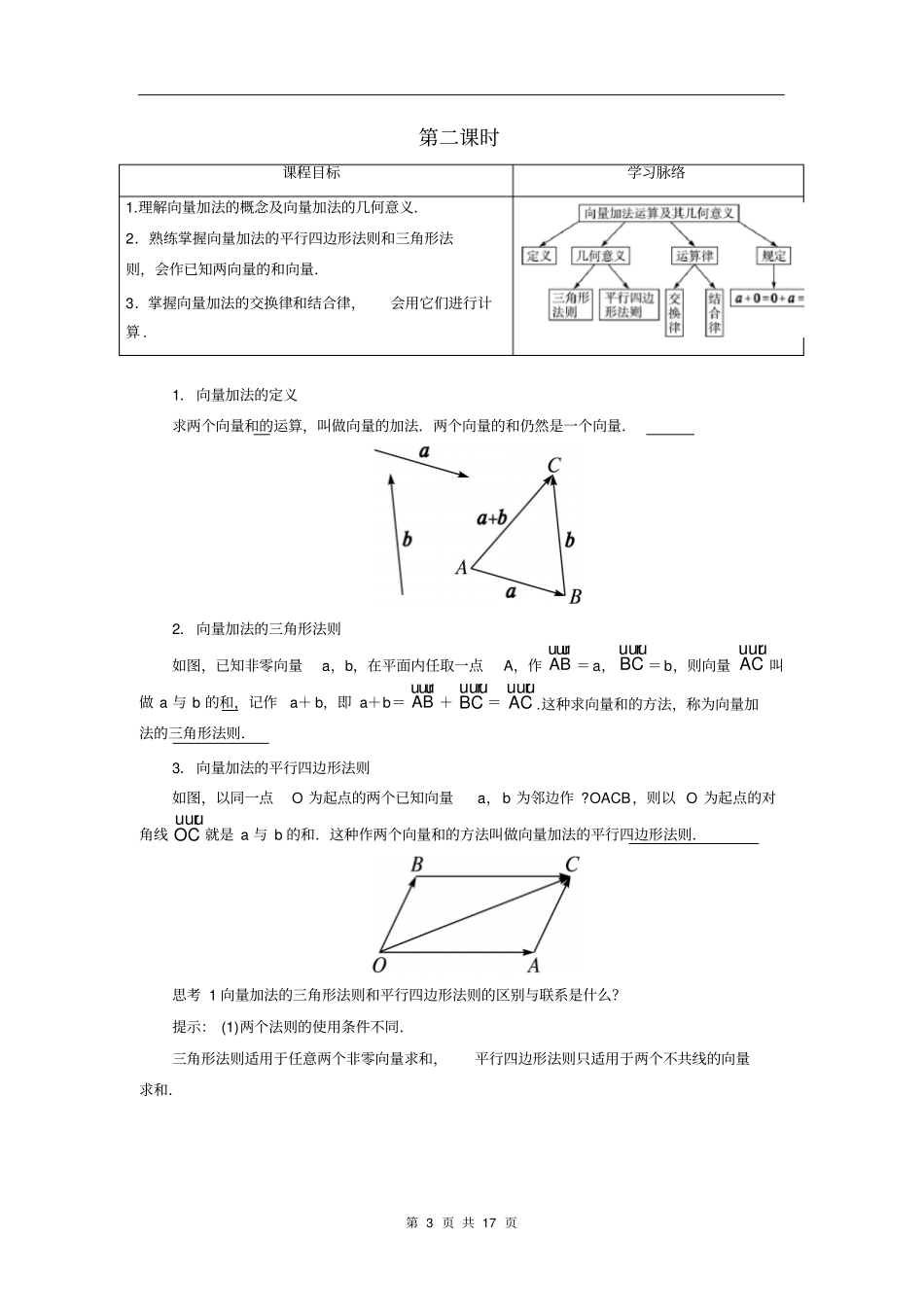
第 1 页 共 17 页第一课时课程目标学习脉络1.了解向量的实际背景,以位移、力等物理背景抽象出向量.2.理解向量、相等向量、共线向量、零向量的概念及向量的表示 .1.向量的概念(1)向量:数学中,我们把既有大小,又有方向的量叫做向量.(2)数量:把那些只有大小,没有方向的量,称为数量.(3)有向线段: 带有方向的线段叫做有向线段,其方向是由起点指向终点.以 A 为起点、B 为终点的有向线段记作ABuuur(如图所示 ),线段 AB 的长度也叫做有向线段ABuuur的长度,记作| ABuuur|.书写有向线段时,起点写在终点的前面,上面标上箭头.(4)有向线段的三个要素:起点、方向、长度.知道了有向线段的起点、方向、长度,它的终点就唯一确定了.思考 1 两个向量可以比较大小吗?提示: 不能.因为向量既有大小,又有方向.2.向量的表示法(1)几何表示:用有向线段表示,此时有向线段的方向就是向量的方向,向量的大小就是向量的长度 (或称模 ),如向量 ABuuur的长度记作 | ABuuur|. (2)字母表示:通常在印刷时,用黑体小写字母a,b,c,⋯表示向量.书写时,可写成带箭头的小写字母ar, br, cr,⋯ .还可以用表示向量的有向线段的起点和终点的字母表示,如以 A 为起点,以B 为终点的向量记为ABuuur. 特别提醒 (1) 向量的书写要规范,如向量a 不能写成 a;(2)向量的起点、终点要搞清,如ABuuur与 BAuuur的起点与终点正好相反.3.有关概念第 2 页 共 17 页思考 2 单位向量都相等吗?提示: 不一定,单位向量的模相等,都等于1,但方向不一定相同.思考 3 表示相等向量的有向线段一定重合吗?提示: 不一定,也可以平行,或在一条直线上.思考 4 共线向量与相等向量有什么关系?提示: 相等向量一定共线,而共线向量不一定相等.特别提醒 (1) 零向量表示为0,而不是数字0;零向量的方向是任意的;规定零向量与任一向量是共线向量.(2)注意向量平行,向量所在直线不一定平行,还有可能是同一条直线.第 3 页 共 17 页第二课时课程目标学习脉络1.理解向量加法的概念及向量加法的几何意义.2.熟练掌握向量加法的平行四边形法则和三角形法则,会作已知两向量的和向量.3.掌握向量加法的交换律和结合律,会用它们进行计算 .1.向量加法的定义求两个向量和的运算,叫做向量的加法.两个向量的和仍然是一个向量.2.向量加法的三角形法则如图,已知非零向量a,b,在平面内任取一点A,作 ABuuur=a,...