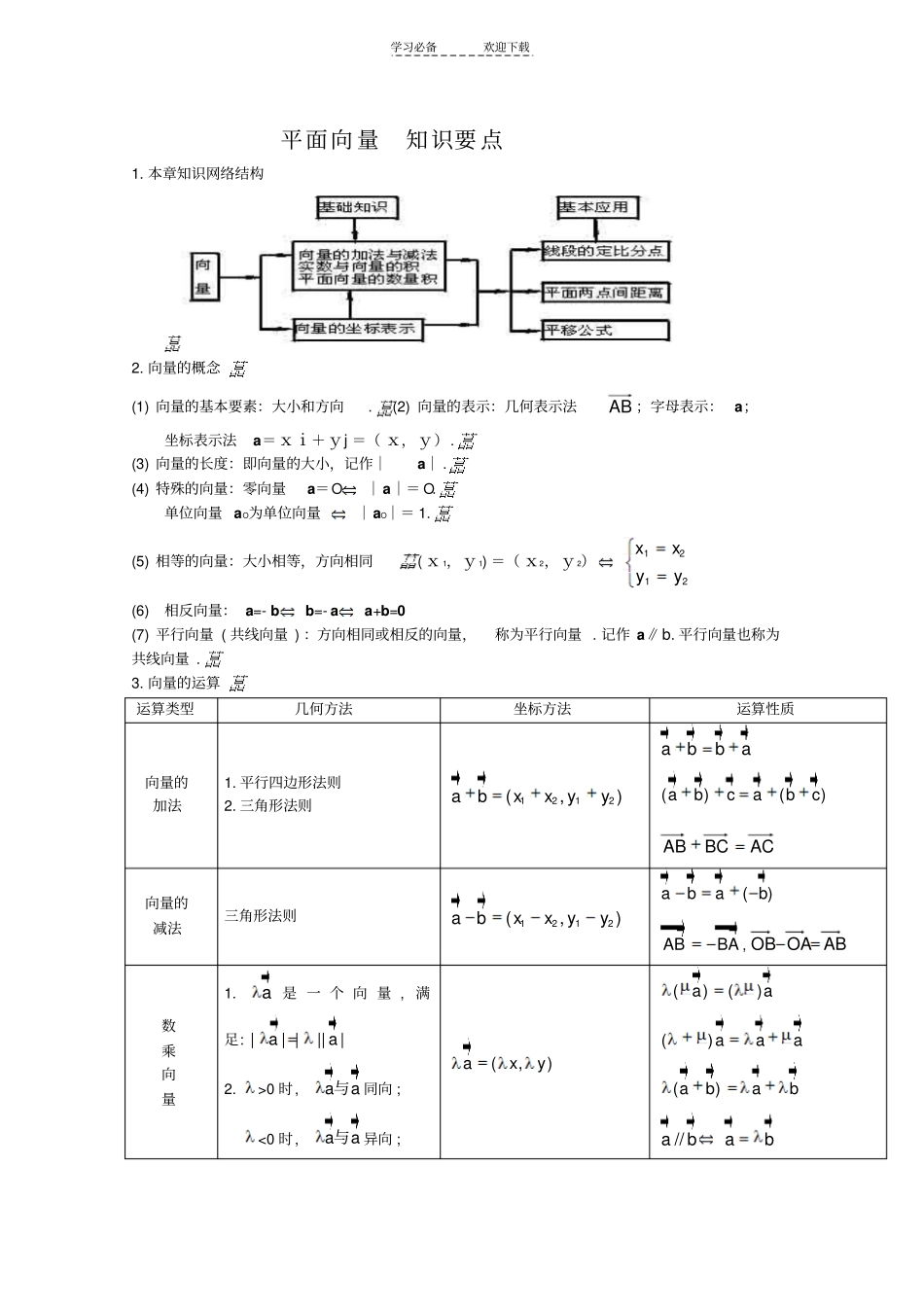
学习必备欢迎下载平面向 量知识要 点1. 本章知识网络结构2. 向量的概念(1) 向量的基本要素:大小和方向.(2) 向量的表示:几何表示法AB ;字母表示: a;坐标表示法a=xi+yj =( x,y).(3) 向量的长度:即向量的大小,记作|a| .(4) 特殊的向量:零向量a=O|a|= O.单位向量 aO为单位向量|aO|= 1.(5) 相等的向量:大小相等,方向相同( x 1,y1) =( x2,y2)2121yyxx(6) 相反向量: a=- bb=- aa+b=0(7) 平行向量 ( 共线向量 ) :方向相同或相反的向量,称为平行向量 . 记作 a∥b. 平行向量也称为共线向量 .3. 向量的运算运算类型几何方法坐标方法运算性质向量的加法1. 平行四边形法则2. 三角形法则1212(,)abxxyyabba()()abcabcACBCAB向量的减法三角形法则1212(,)abxxyy()ababABBA ,ABOAOB数乘向量1.a 是 一 个 向 量 , 满足: || ||||aa2.>0 时, aa与同向 ; <0 时, aa与异向 ; (,)axy()()aa()aaa()abab//abab学习必备欢迎下载=0 时, 0a. 向量的数量积a b 是一个数1.00ab或时,0ab. 2.00|||| cos( , )aba ba ba b且时,1212a bx xy ya bb a()()()ababa b()abcacbc2222||| |=aaaxy即|| ||||abab4. 重要定理、公式(1) 平面向量基本定理e1,e2是同一平面内两个不共线的向量,那么,对于这个平面内任一向量,有且仅有一对实数 λ1,λ2,使 a=λ1e1+λ2e2.(2) 两个向量平行的充要条件a∥ba=λ b(b≠0)x1y2-x2y1=O.(3) 两个向量垂直的充要条件a⊥ba·b=Ox1x2+y1y2=O.(4) 线段的定比分点公式设点 P分有向线段21PP所成的比为 λ ,即PP1= λ2PP ,则OP =111OP +112OP ( 线段的定比分点的向量公式).1,12121yyyxxx ( 线段定比分点的坐标公式)当λ =1 时,得中点公式:OP =21 (1OP +2OP )或.2,22121yyyxxx (5) 平移公式设点 P( x,y) 按向量 a=( h,k)平移后得到点P′ ( x′ , y′ ),学习必备欢迎下载则PO= OP +a 或.,kyyhxx曲线 y=f(x)按向量 a=( h,k)平移后所得的曲线的函数解析式为:y-k=f(x-h) (6) 正、余弦定理正弦定理:.2sinsinsinRCcBbAa余弦定理: a2=b2+c2-2bccosA,b2=c2+a2-2cacosB,c2=a2+b2-2abcosC.(7)三角形面积计算公式:设△ ABC的三边为 a,b,c,其高分别为ha,hb,hc,半周长为 P,外接圆、 内切圆的半径为R,r. ①S△=1/2aha=...