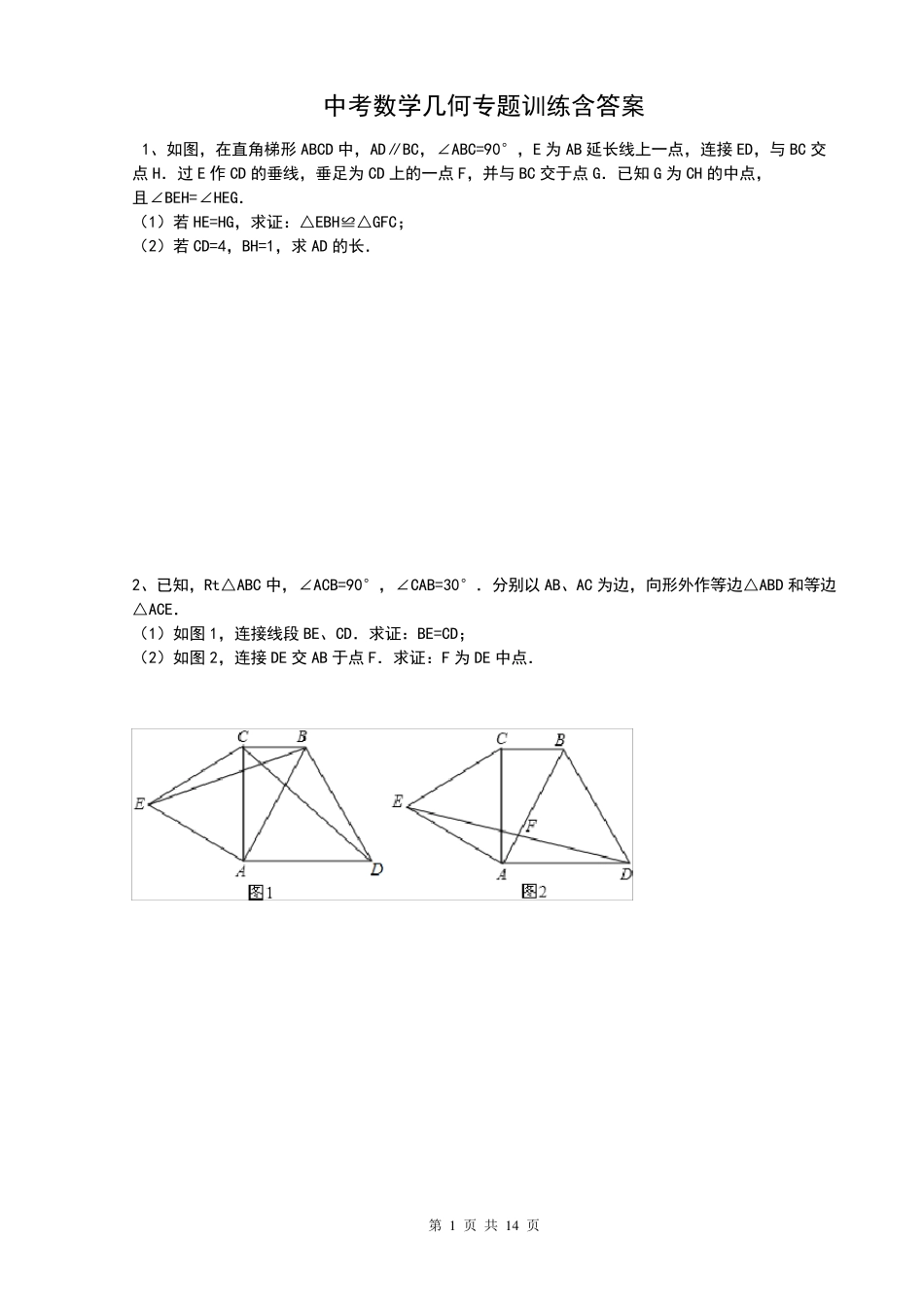
第 1 页 共 1 4 页 中考数学几何专题训练含答案 1、如图,在直角梯形ABCD 中,AD∥BC,∠ABC=90°,E 为 AB 延长线上一点,连接 ED,与 BC 交 点 H.过 E 作 CD 的垂线,垂足为 CD 上的一点 F,并与 BC 交于点 G.已知 G 为 CH 的中点, 且∠BEH=∠HEG. (1)若 HE=HG,求证:△EBH≌△GFC; (2)若 CD=4,BH=1,求 AD 的长. 2、已知,Rt△ABC 中,∠ACB=90°,∠CAB=30°.分别以 AB、AC 为边,向形外作等边△ABD 和等边△ACE. (1)如图1,连接线段 BE、CD.求证:BE=CD; (2)如图2,连接 DE 交 AB 于点 F.求证:F 为 DE 中点. 第 2 页 共 14 页 3、如图,在梯形ABCD 中,AD∥BC,∠C=90°,E 为 CD 的中点,EF∥AB 交 BC 于点 F (1)求证:BF=AD+CF; (2)当 AD=1,BC=7,且 BE 平分∠ABC 时,求 EF 的长. 4、在等腰梯形ABCD 中,AD∥BC,AB=AD=CD,∠ABC=60°,延长 AD 到 E,使 DE=AD,延长 DC 到 F,使 DC=CF,连接 BE、BF 和 EF. ⑴求证:△ABE≌△CFB; ⑵如果 AD=6,tan∠EBC 的值. A B D E C F 第 3 页 共 14 页 5、已知:AC 是矩形ABCD 的对角线,延长CB 至E,使CE=CA,F 是AE 的中点,连接DF、CF分别交AB 于G、H 点(1)求证:FG=FH;(2)若∠E=60°,且AE=8 时,求梯形AECD 的面积. 6、如图,直角梯形ABCD 中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2,过点D 作 DE∥AB,交∠BCD 的平分线于点E,连接BE. (1)求证:BC=CD; (2)将△BCE 绕点C,顺时针旋转 90°得到△DCG,连接EG.求证:CD 垂直平分EG; (3)延长BE 交CD 于点P.求证:P 是CD 的中点. 第 4 页 共 14 页 7、如图,直角梯形ABCD 中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60 度.以 AD 为边在直角梯形ABCD 外作等边三角形ADF,点 E 是直角梯形ABCD 内一点,且∠EAD=∠EDA=15°,连接 EB、EF. (1)求证:EB=EF; (2)延长 FE 交 BC 于点 G ,点 G 恰好是 BC 的中点,若 AB=6,求 BC 的长. (1)证明: △ADF 为等边三角形, 8、已知,矩形ABCD 中,延长 BC 至 E,使 BE=BD,F 为 DE 的中点,连结 AF、CF.求证: (1)∠ADF=∠BCF; (2) AF⊥CF. 9、如图,在直角梯形ABCD 中,AD⊥DC,AB∥DC,AB=BC,AD 与 BC 延长线交于点 F,G 是DC 延长线上一点,AG ⊥B...